如图,直线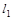 :
: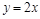 与直线
与直线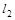 :
: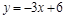 相交于点
相交于点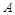 ,直线
,直线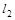 与
与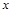 轴交于点
轴交于点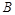 ,平行于
,平行于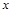 轴的直线
轴的直线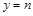 分别交直线
分别交直线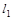 、直线
、直线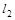 于
于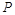 、
、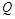 两点(点
两点(点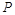 在
在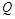 的左侧)
的左侧)
⑴点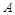 的坐标为 ;
的坐标为 ;
⑵如图1,若点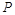 在线段
在线段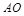 上,在
上,在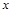 轴上是否存在一点
轴上是否存在一点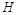 ,使得
,使得 为等腰直角三角形,若存在,求出点
为等腰直角三角形,若存在,求出点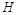 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
⑶如图2.若以点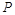 为直角顶点,向下作等腰直角
为直角顶点,向下作等腰直角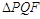 ,设
,设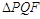 与
与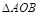 重叠部分的面积为
重叠部分的面积为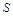 ,求
,求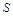 与
与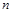 的函数关系式;并注明
的函数关系式;并注明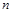 的取值范围.
的取值范围.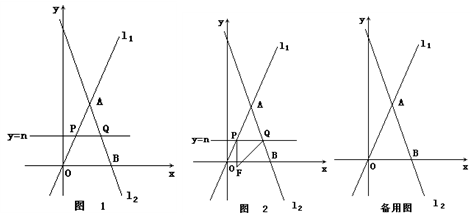
相关知识点
推荐套卷
如图,直线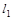 :
: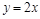 与直线
与直线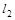 :
: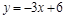 相交于点
相交于点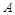 ,直线
,直线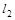 与
与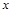 轴交于点
轴交于点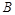 ,平行于
,平行于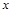 轴的直线
轴的直线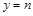 分别交直线
分别交直线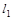 、直线
、直线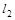 于
于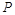 、
、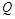 两点(点
两点(点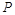 在
在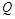 的左侧)
的左侧)
⑴点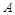 的坐标为 ;
的坐标为 ;
⑵如图1,若点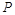 在线段
在线段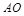 上,在
上,在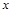 轴上是否存在一点
轴上是否存在一点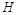 ,使得
,使得 为等腰直角三角形,若存在,求出点
为等腰直角三角形,若存在,求出点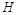 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
⑶如图2.若以点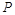 为直角顶点,向下作等腰直角
为直角顶点,向下作等腰直角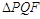 ,设
,设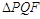 与
与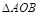 重叠部分的面积为
重叠部分的面积为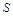 ,求
,求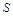 与
与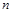 的函数关系式;并注明
的函数关系式;并注明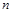 的取值范围.
的取值范围.