初中数学一次函数的最值解答题

游泳池常需进行换水清洗，图中的折线表示的是游泳池换水清洗过程“排水﹣﹣清洗﹣﹣灌水”中水量y（m³）与时间t（min）之间的函数关系式．
（1）根据图中提供的信息，求整个换水清洗过程水量y（m³）与时间t（min）的函数解析式；
（2）问：排水、清洗、灌水各花多少时间？

科学研究发现，空气含氧量（克/立方米）与海拔高度（米）之间近似地满足一次函数关系．经测量，在海拔高度为0米的地方，空气含氧量约为299克/立方米；在海拔高度为2000米的地方，空气含氧量约为235克/立方米．
（1）求出与的函数表达式；
（2）已知某山的海拔高度为1200米，请你求出该山山顶处的空气含氧量约为多少？

如图，在平面直角坐标系中，已知点A(2，3)、B(6，3)，连结AB. 如果点P
在直线y＝x－1上，且点P到直线AB的距离小于1，那么称点P是线段AB的“邻近点”．
（1）判断点Ｃ(， ) 是否是线段AB的“邻近点”，并说明理由；
（2）若点Q (m，n)是线段AB的“邻近点”，求m的取值范围．

如图，已知，是一次函数的图像和反比例函数的图像的
两个交点．

（1）求反比例函数和一次函数的解析式；
（2）求直线与轴的交点的坐标及三角形的面积．
（3）当为何值时，一次函数的值小于反比例函数的值？

已知函数，与成正比例，与成反比例，且当时，；当时，．（1）求与的函数关系式;（2）当时，求的值．

已知一次函数与反比例函数的图象交于点．
（1）求这两个函数的函数关系式；
（2）在给定的直角坐标系（如图）中，画出这两个函数的大致图象；
（3）当为何值时，一次函数的值大于反比例函数的值？

如图，在平面直角坐标系中，点P是第一象限直线上的点，点A，O是坐标原点，△PAO的面积为.

⑴求与的函数关系式,并写出x的取值范围；
⑵探究：当P点运动到什么位置时△PAO的面积为10.

某公司有型产品40件，型产品60件，分配给下属甲、乙两个商店销售，其中70件给甲店，30件给乙店，且都能卖完．两商店销售这两种产品每件的利润（元）如下表：

	型利润	型利润
甲店	200	170
乙店	160	150

 
（1）设分配给甲店型产品件，这家公司卖出这100件产品的总利润为y（元），求y关于的函数关系式，并求出的取值范围；
（2）若公司要求总利润不低于17560元，有多少种不同分配方案，哪种方案总利润最大，并求出最大值。

某人从离家18千米的地方返回，他离家的距离s(千米)与时间t(分钟)的函数图象如图所示：⑴求线段AB的解析式；⑵求此人回家用了多长时间？

已知甲乙两种食物中维生素A和B的含量及甲乙食物的成本如下表：

	甲	乙
维生素A（单位/千克）	300	500
维生素B（单位/千克）	700	100
成本（元/千克）	5	4

现将两种食物混合成100千克的混合食品。设混合食品中甲、乙食物含量分别为x（千克）和y（千克），如果混合食品中要求维生素A不低于40000单位，B不低于28000单位
（1）求x的取值范围
（2）当甲、乙各取多少千克时，符合题意的混合食品成本最低？并求该最低成本价

某种子商店销售“黄金一号”玉米种子，为惠民促销，推出两种销售方案供采购者选择。
方案一：每克种子价格为4元，无论购买多少均不打折；
方案二：购买3千克以内（含3千克）的价格为每千克5元，若一次性购买超过3千克的，则超过3千克的部分的，则超过3千克的部分的种子价格打7折。
（1）请分别求出方案一和方案二中购买的种子数量x（千克）和付款金额．y（元）之间的函数关系式；
（2）若你去购买一定量的种子，你会怎样选择方案？说明理由。

现有一个种植总面积为540m²的矩形塑料温棚，分垄间隔套种草莓和西红柿共24垄，种植的草莓或西红柿单种农作物的总垄数不低于10垄，又不超过14垄(垄数为正整数)，它们的占地面积、产量、利润分别如下：

	占地面积（m/垄）	产量（千克/垄）	利润（元/千克）
西红柿	30	160	1.1
草莓	15	50	1.6

（1）若设草莓共种植了垄，通过计算说明共有几种种植方案？分别是哪几种？
（2）在这几种种植方案中，哪种方案获得的利润最大？最大利润是多少？

大学生王强积极响应“自主创业”的号召，准备投资销售一种进价为每件40元
的小家电.通过试营销发现，当销售单价在40元至90元之间（含40元和90元）时，每月的销售量y（件）
与销售单价x（元）之间的关系可近似地看作一次函数，其图象如图所示.
（1）求y与x的函数关系式.
（2）设王强每月获得的利润为p（元）,求p与x之间的函数关系式；如果王强想要每月获得2400元的
利润，那么销售单价应定为多少元？

某市为创建省卫生城市，有关部门决定利用现有的4200盆甲种花卉和3090盆乙种花卉，搭配A、B两种园艺造型共60个，摆放于入城大道的两侧，搭配每个造型所需花卉数量的情况下表所示，结合上述信息，解答下列问题：
（1）符合题意的搭配方案有几种？
（2）如果搭配一个A种造型的成本为1000元，搭配一个B种造型的成本为1500元，试说明选用那种方案成本最低？最低成本为多少元？

造型花卉	甲	乙
A	80	40
B	50	70

“节能环保，低碳生活”是我们倡导的一种 生活方式，某家电商场计划用11.8万元购进节能型电视机、洗衣机和空调共40台，三种家电的进价和售价如下表所示：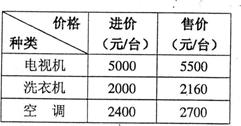

（1）在不超出现有资金前提下，若购进电视机的数量和洗衣机的数量相同，空调的数量不超过电视机的数量的3倍．请问商场有哪几种进货方案？
（2）在“2012年消费促进月”促销活动期问，商家针对这三种节能型)品推出“现金每购满1000元送50元家电消费券一张、多买多送”的活动．在(1)的条件下若三种电器在活动期间全部售出，商家预估最多送出消费券多少张？