初中数学一次函数的最值解答题

如图，一次函数的图象与x轴、y轴分别相交于A、B两点，且与反比例函数（）的图象在第一象限交于点C，如果点B的坐标为（0，2），OA=OB，B是线段AC的中点．

（1）求点A的坐标及一次函数解析式．
（2）求点C的坐标及反比例函数的解析式．

为推进节能减排，发展低碳经济，江阴某公司以25万元购得某项节能产品的生产技术后，再投入100万元购买生产设备，进行该产品的生产加工．已知生产这种产品的成本价为每件20元．经过市场调研发现，该产品的销售单价定在25元到30元之间较为合理，并且该产品的年销售量y（万件）与销售单价x（元）之间的函数关系式为：（年获利=年销售收入—生产成本—投资成本）
（1）当销售单价定为28元时，该产品的年销售量为多少万件？
（2）求该公司第一年的年获利W（万元）与销售单价x（元）之间的函数关系式，并说明投资的第一年，该公司是盈利还是亏损？若盈利，最大利润是多少？若亏损，最小亏损是多少？
（3）第二年，该公司决定给希望工程捐款Z万元，该项捐款由两部分组成：一部分为10万元的固定捐款；另一部分则为每销售一件产品，就抽出一元钱作为捐款．若除去第一年的最大获利（或最小亏损）以及第二年的捐款后，到第二年年底，两年的总盈利不低于67．5万元，请你确定此时销售单价的范围．

如图，已知点A（a，3）是一次函数y₁=x+b图象与反比例函数y₂=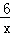图象的一个交点．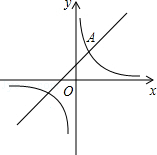

（1）求一次函数的解析式；
（2）在y轴的右侧，当y₁＞y₂时，直接写出x的取值范围．

（本小题满分13分）如图，矩形OABC的顶点A、C分别在x轴和y轴上，点B的坐标为（2，3），双曲线，的图像经过BC上的点D与AB交于点E，连接DE，若若E是AB的中点﹒

（1）求D点的坐标；
（2）点F是OC边上一点，若△FBC和△DEB相似，求BF的解析式；
（3）若点P（m，3m+6）也在此反比例函数的图像上（其中m >0），过p点作x轴的垂线，交x轴于点M，若线段PM上存在一点Q，使得△OQM的面积是，设Q点的纵坐标为n，求的值．

如图，直线AB与x轴交于点A（1，0），与y轴交于点B（0，-2）．

（1）求直线AB的解析式；
（2）直线AB上是否存在点C，使△BOC的面积为2？若存在，求出点C的坐标；若不存在，请说明理由．

已知函数与函数交于点A（2，b）B（-3，m）两点（点A在第一象限），

（1）求b，m，k的值；
（2）函数 与x轴交于点C，求△ABC的面积．

如图，一次函数y＝x＋6与反比例函数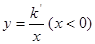的图象相交于A，B两点，与x轴、y轴交于E、F，点B的横坐标为。

（1）试确定反比例函数的解析式；
（2）求点E、F的坐标。

（本小题满分7分）已知某企业2014年用水量x（吨）与该月应交的水费y（元）之间的函数关系如图．

（1）求2014年水费y（元）关于x（吨）的函数关系式；
（2）为贯彻省委“五水共治”发展战略，鼓励企业节约用水，该市自2015年1月开始对月用水量超过96吨的企业加收污水处理费，规定：若企业月用水量x超过96吨，则除按2014年收费标准收取水费外，超过96吨部分每吨另加收元．这样企业每月“用水费用”就可能包括水费和污水处理费．求2015年水费y（元）关于x（吨）的函数关系式．

（本题10分）已知直线y＝－x＋4与x轴和y轴分别交与B、A两点，另一直线经过点B和点D（11,6）．

（1）求A、B的坐标；
（2）证明：△ABD是直角三角形；
（3）在x轴上找点C，使△ACD是以AD为底边的等腰三角形，求出C点坐标．

如图：一次函数的图像与x轴、y轴分别交于A、B两点，且A、B两点的坐标分别为（4，0），（0，3）．

（1）求一次函数的表达式．
（2）点C在线段OA上，沿BC将△OBC翻折，O点恰好落在AB上的D处，求直线BC的表达式．

如图，直线l：与x轴交于点A，与y轴交于点B．

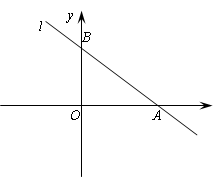
（1）求点A与点B的坐标；
（2）直线m与直线l平行，且与x轴交于点C，与y轴交于点D，若使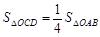，求直线m的解析式．

如图，平面直角坐标系xOy中，一次函数y=-x+b（b为常数，b＞0）的图象与x轴、y轴分别相交于点A、B，半径为4的⊙O与x轴正半轴相交于点C，与y轴相交于点D、E，点D在点E上方．

（1）若直线AB与有两个交点F、G．
①求∠CFE的度数；
②用含b的代数式表示FG²，并直接写出b的取值范围；
（2）设b≥5，在线段AB上是否存在点P，使∠CPE=45°？若存在，请求出P点坐标；若不存在，请说明理由．

如图，和分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系。

（1）B出发时与A相距           千米；
（2）B走了一段路后，自行车发生故障，进行修理，所用的时间是          小时；
（3）B出发后           小时与A相遇；
（4）若B的自行车不发生故障，保持出发时的速度前进，那么B几小时后与A相遇，相遇点离B的出发点多少千米？在图中标出这个相遇点C.

（本小题满分6分）已知一次函数的图像经过点（－2，4），且与正比例函数的图像平行．
（1） 求一次函数的解析式；
（2） 求一次函数的图像与坐标轴所围成的三角形的面积；
（3） 若A（a，），B（a＋b，）为一次函数的图像上两个点，试比较与的大小．

已知一次函数y=kx+b的图象经过点（-1，-5），且与正比例函数的图象相交于点（2，a）．
（1）求a的值．
（2）求一次函数y=kx+b的表达式．
（3）在同一坐标系中，画出这两个函数的图象．