初中数学一次函数的最值解答题

如图,在平面直角坐标系xOy中，函数y=（x＞0）的图像与一次函数y=kx-k的图像的交点为A（m，3）．

（1）求一次函数的解析式；
（2）设一次函数y=kx-k的图像与y轴交于点B，若点P是x轴上一点，且满足△PAB的面积是9，直接写出P点的坐标．

一次函数y=kx+4的图象经过点（－3，－2），则
（1）求这个函数表达式；
（2）判断（－5，3）是否在此函数的图象上;

填表，并在同一坐标系内作出函数 和的图像；
填表：                       作图区：

x	…	0		…
y	…		0	…

 

x	…	0		…
y	…		0	…

已知一次函数图象经过点A（2，1）和点（－2，5），求这个一次函数的解析式.

已知一次函数的图象经过（1，3）和（-2，0）两点，求关于的方程的根

已知一次函数 的图象经过点．
（1）求出的值；
（2）求当=1时，的值．

已知与成正比例,且时,.
(1)求与的函数关系式; 
(2)当时,求的值;
(3)将所得函数图象平移,使它过点(2, －1).求平移后直线的解析式.

正比例函数 y＝kx 和一次函数 y＝ax＋b的图象都经过点 A(1,2)，且一次函数的图象交 x 轴于点 B(4,0)．求正比例函数和一次函数的表达式．

一次函数y =的图象经过第一、二、四象限，求m的取值范围 .

已知y＋2与x成正比例，且x=-2时，y=0.求y与x的函数关系式.

已知：点A（2，－2）和点B（1，－4）在一次函数的图象上，
（1）求和的值；
（2）求当x＝时的函数值．

某小区有一长100m，宽80m的空地，现将其建成花园广场，设计图案如下：阴影区域为绿化区（四块绿化区是全等矩形），空白区域为活动区，且四周出口一样宽，宽度不小于50m，不大于60m．预计活动区每平方米造价60元，绿化区每平方米造价50元．

（1）设一块绿化区的长边为xm，写出工程总造价y与x的函数关系式（写出x的取值范围）．
（2）如果小区投资46.9万元，问能否完成工程任务？若能，请写出x为整数的所有工程方案；若不能，请说明理由．（参考值： 3≈1.732）

已知一次函数的图象与双曲线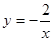交于两点的坐标分别为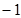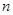（，）、（，－1）；
求该一次函数的解析式
描出函数草图，根据图象写出使一次函数的值大于反比例函数的值的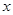的取值范围.

如图，一次函数y=kx+b的图象与反比例函数y=的图象交于
A（-2，1）B（1，n）两点．

试确定上述反比例函数和一次函数的表达式
求△ABO的面积
根据图像直接写出当一次函数的值大于反比例函数的值时
x的取值范围。

已知：直线与轴交于点A，与轴交于点B．
（1）分别求出A，B两点的坐标
（2）过A点作直线AP与轴交于点P，且使OP=2OB，求△ABP的面积