初中数学一次函数的最值选择题

如图，已知直线y₁=x+m与y₂=kx-1相交于点P（-1，1），关于x的不等式x+m＞kx-1的解集是（   ）

A．x≥-1

B．x＞-1

C．x≤-1

D．x＜-1

童童从家出发前往奥体中心观看某演出，先匀速步行至轻轨车站，等了一会儿，童童搭乘轻轨 至奥体中心观看演出，演出结束后，童童搭乘邻居刘叔叔的车顺利到家．其中x表示童童从家出发后所用时间，y表示童童离家的距离．下图能反映y与x的函数关系式的大致图象是（    ）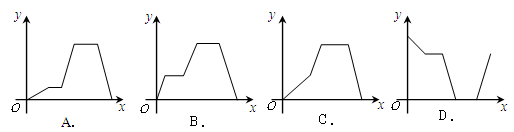

如图，过A点的一次函数的图象与正比例函数y=2x的图象相交于点B，则这个一次函数的解析式是（ ）
 

A．y="2x+3"

B．y=x﹣3

C．y=2x﹣3

D．y=﹣x+3

为使我市冬季“天更蓝、房更暖”、政府决定实施“煤改气”供暖改造工程，现甲、乙两工程队分别同时开挖两条600米长的管道，所挖管道长度y（米）与挖掘时间x（天）之间的关系如图所示，则下列说法中：
①甲队每天挖100米；
②乙队开挖两天后，每天挖50米；
③当x=4时，甲、乙两队所挖管道长度相同；
④甲队比乙队提前2天完成任务．
正确的个数有（　　）

A．1个

B．2个

C．3个

D．4个

一个装有进水管和出水管的容器，从某时刻开始的4分钟内只进水不出水，在随后的8分钟内既进水又出水，假设每分的进水量和出水量是两个常数，容器内的水量y（单位：升）与时间x（单位：分）之间的关系如图．则每分钟的进水量与出水量分别是（　　）

A．5、2.5

B．20、10

C．5、3.75

D．5、1.25

已知一次函数的图象与直线y=-x+1平行，且过点（8，2），那么此一次函数的解析式为（　　）

A．y=-x-2

B．y=-x-6

C．y=-x+10

D．y=-x-1

已知过点的直线不经过第一象限.设，则s的取值范围是（  ）

A．

B．

C．

D．

在直角坐标系中，一直线a向下平移3个单位后所得直线b经过点A（0，3），将直线b绕点A顺时针旋转60°后所得直线经过点B（，0），则直线a的函数关系式为（  ）

A．

B．

C．

D．

甲,乙两人以相同路线前往距离单位10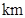的培训中心参加学习.图中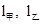分别表示甲，乙两人前往目的地所走的路程s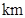随时间(分)变化的函数图象.以下说法：①乙比甲提前12分钟到达；②甲的平均速度为15千米/小时；③乙走了8后遇到甲;④乙出发6分钟后追上甲.其中正确的有（  ）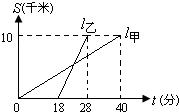

A．4个

B．3个

C．2个

D．1个

已知点A的坐标为（2，0），点P在直线y=x上运动，当以点P为圆心，PA的长为半径的圆的面积最小时，点P的坐标为（　　）

A．（1，﹣1）

B．（0，0）

C．（1，1）

D．（，）

如图，函数y=2x和y=ax+4的图象相交于点A（m，3），则不等式2x≥ax+4的解集为（　　）

A．x≥

B．x≤3

C．x≤

D．x≥3

在一次测验中的解答的填空题如下：
（1）当m取1时，一次函数y=（m﹣2）x+3，y随x的增大而增大；
（2）等腰梯形ABCD，上底AD=2，下底BE=8，∠B=60°，则腰长AB=6； 
（3）菱形的边长为6cm，一组相邻角的比为l：2，则菱形的两条对角线的长分别为6cm和6cm； 
（4）如果一个多边形的内角和比它的外角和的3倍少180°，则这个多边形是五边形． 
你认为正确的填空个数是（ ）

A．1个

B．2个

C．3个

D．4个

已知点A在双曲线上，点B在直线上，且A，B两点关于轴对称，设点A的坐标为（，），则+的值是(  )

A．-10

B．-8

C．6

D．4

“黄金1号”玉米种子的价格为5元/千克，如果一次购买2千克以上的种子，超过2千克部分的种子的价格打6折，设购买种子数量为千克，付款金额为元，则与的函数关系的图像大致是  (  )

（A）           （B）             （C）           （D）

2013年4月20日08时02分在四川雅安芦山县发生7.0级地震，人民生命财产遭受重大损失．某部队接到上级命令，乘车前往灾区救援，前进一段路程后，由于道路受阻，车辆无法通行，通过短暂休整后决定步行前往．则能反映部队与灾区的距离（千米）与时间（小时）之间函数关系的大致图象是（　　）

A．              B．                   C．                D．