山西省孝义市八年级下学期期末考试数学试卷
下列函数中,自变量x的取值范围是x≥3的是( )
A.y=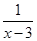 |
B.y=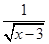 |
C.y=x﹣3 | D.y= |
一次函数y=kx+b中,y随x的增大而增大,b<0,则这个函数的图象不经过( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
若直线y=(m﹣2)x﹣6与x轴的交点是(6,0),则m的值是( )
| A.3 | B.2 | C.1 | D.0 |
线段a、b、c组成的三角形不是直角三角形的是( )
| A.a=7,b=24,c=25 | B.B a= ,b=4,c=5 ,b=4,c=5 |
C.a= ,b=1,c= ,b=1,c= |
D.a=40,b=50,c=60 |
下列四边形中,对角线相等且互相垂直平分的是( )
| A.平行四边形 | B.正方形 | C.等腰梯形 | D.矩形 |
一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,假设每分的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图.则每分钟的进水量与出水量分别是( )
| A.5、2.5 | B.20、10 | C.5、3.75 | D.5、1.25 |
某班60名学生喜欢各类体育活动,他们最喜欢的一项体育活动情况见扇形统计图,现给出以下说法
①最受欢迎的球类运动是乒乓球;
②最喜欢排球的学生达到班级学生总数的;
③最喜欢羽毛球的学生达到班级学生总数的12人.
④最喜欢其他运动的学生达到12%
其中正确的结论为( )
| A.①②③ | B.①③④ | C.①②④ | D.①②③④ |
甲、乙二人各射击5次,命中环数如下表
| |
第1次 |
第2次 |
第3次 |
第4次 |
第5次 |
| 甲 |
7 |
8 |
6 |
8 |
6 |
| 乙 |
9 |
5 |
6 |
7 |
8 |
那么射击技术稳定的是 _________ .
已知直线y=kx+b经过两点(3,6)和(﹣1,﹣2),则直线的解析式为 _________ .
已知直线y=3x+k与x轴交于(﹣2,0),则不等式3x+k≤0的解集是 _________ .
如图,平行四边形ABCD的对角线AC、BD交于一点O,AB=11,△OCD的周长为27,则AC+BD= _________ .
如图,将两条宽度都是为2的纸条重叠在一起,使∠ABC=45°,则四边形ABCD的面积为 _________ .
如图,在平面直角坐标系中,直线y=﹣x+6与x轴交于点B,与y轴交于点A,点C是线段AB的中点,则OC的长是 _________ .
图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,点A和点B在小正方形的顶点上.
(1)在图1中画出△ABC(点C在小正方形的顶点上),使△ABC为直角三角形(画一个即可);
(2)在图2中画出△ABD(点D在小正方形的顶点上),使△ABD为等腰三角形(画一个即可).
为了提高农民收入,村干部带领村民自愿投资办起了一个养鸡场,办场时买来的3000只小鸡,经过一段时间的精心饲养,可以出售了.下表是从中抽取的100只鸡出售时质量的统计数据.
| 质量 |
1.0 |
1.2 |
1.5 |
1.8 |
2.0 |
| 频数 |
11 |
23 |
32 |
24 |
10 |
(1)写出抽取的这100只鸡出售时质量的众数与中位数,并求这出售的100只鸡的平均质量是多少?(结果保留小数点后一位)
(2)根据市场价格,利润是4元/kg,请你估计这3000只鸡全部出售,可以获得的利润是多少元?
(3)本题(2)中用到的统计思想是什么?
如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AM∥BD,交CB的延长线于点M.
(1)求证:△ADE≌△CBF;
(2)若四边形是BEDF菱形,AD=3,∠ABD=30°,求四边形AMBD的面积.
如表,给出A、B两种上网宽带的收费方式:
| 收费方式 |
月使用费/元 |
包月上网时间/小时 |
超时费/(元/分) |
| A |
30 |
20 |
0.05 |
| B |
60 |
不限时 |
|
假设月上网时间为x小时,方式A、B的收费方式分别是yA(元)、yB(元).
(1)请写出yA、yB分别与x的函数关系式,并写出自变量的范围(注意结果要化简);
(2)在给出的坐标系中画出这两个函数的图象;
(3)结合图象与解析式,填空:
当上网时间x的取值范围是 _________ 时,选择方式A省钱;
当上网时间x的取值范围是 _________ 时,选择方式B省钱.
提出问题:如图1,将三角板放在正方形ABCD上,使三角板的直角顶点P在对角线AC上,一条直角边经过点B,另一条直角边交边DC与点E,求证:PB=PE
分析问题:学生甲:如图1,过点P作PM⊥BC,PN⊥CD,垂足分别为M,N通过证明两三角形全等,进而证明两条线段相等.
学生乙:连接DP,如图2,很容易证明PD=PB,然后再通过“等角对等边”证明PE=PD,就可以证明PB=PE了.
解决问题:请你选择上述一种方法给予证明.
问题延伸:如图3,移动三角板,使三角板的直角顶点P在对角线AC上,一条直角边经过点B,另一条直角边交DC的延长线于点E,PB=PE还成立吗?若成立,请证明;若不成立,请说明理由.
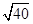 的结果是( )
的结果是( )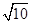
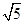
 ﹣2的乘积是有理数的是( )
﹣2的乘积是有理数的是( )
 =_________.
=_________. ;
; +(y﹣
+(y﹣ )2=0,求
)2=0,求 的值.
的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号