在平面直角坐标系中，已知点A（
，0），B（2，0），若点C在一次函数
的图象上，且△ABC为直角三角形，则满足条件的点C有 （ ）
| A．1个 | B．2个 | C．3个 | D．4个 |
在数-1，1，2中任取两个数作为点坐标，那么该点刚好在一次函数
图象上的概率是（ ）。
A．  |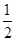
B． |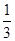
C． |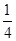
D． |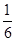
下列四个命题：
①如果不等式组
的解集为x>3，则m≤3；
②若关于
的分式方程
有增根，则m=1；
③反比例函数
与正比例函数
的图象交于点A、B，点A的坐标为(1，-3)，若则点B坐标为（-1，3）；
④二次函数y=ax2+bx+c的值恒为正，则a,b,c应满足a>0，b2-4ac<0 ．
其中正确命题的个数为
A．1个 B．2个 C．3个 D．4个
2014年3月31日凌晨，重庆东水门长江大桥正式通车，重庆主城再添一座跨江大桥，为重庆的经济发展提供了帮助.王大爷为了感受重庆交通的发展，搭乘公交车从家去参观东水门长江大桥，预计1个小时能到达．行驶了半个小时，刚好行驶了一半路程，遇到堵车道路被“堵死”，堵了几分钟突然发现旁边刚好有一个轻轨站，于是王大爷转乘轻轨去观看大桥(轻轨速度大于公交车速度)，结果按预计时间到达．下面能反映王大爷距大桥的距离
（千米）与时间
（小时）的函数关系的大致图象是（ ）
A. B. C. D.
把直线y＝－x－3向上平移m个单位后，与直线y＝2x＋4的交点在第二象限，则m的取值范围是( )
| A．1＜m＜7 | B．3＜m＜4 | C．m＞1 | D．m＜4 |
直线l1：y=k1x+b与直线l2：y=k2x在同一平面直角坐标系中的图象如图所示，则关于x的不等式k1x+b＞k2x的解为（ ）
| A．x＞-1 | B．x＜-1 |
| C．x＜-2 | D．无法确定 |
某人骑车沿直线旅行，先前进了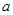
千米，休息了一段时间，又原路原速返回了
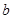千米（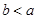
），再掉头沿原方向以比原速大的速度行驶，则此人离起点的距离
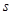与时间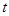
的函数关系的大致图象是（ ）.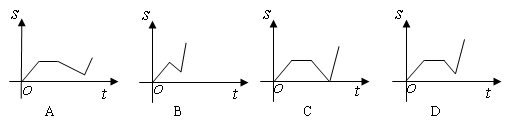
小文、小亮从学校出发到青少年宫参加书法比赛,小文步行一段时间后, 小亮骑自行车沿相同路线行进,两人均匀速前行．他们的路差s(米)与小文出发时间t(分)之间的函数关系如图所示．下列说法：①小亮先到达青少年宫; ②小亮的速度是小文速度的2．5倍; ③a="24;" ④b=480．其中正确的是的 （ ）．
| A．①②③ | B．①②④ | C．①③④ | D．①②③④ |
一辆汽车和一辆摩托车分别从
两地去同一城市,它们离
地的路程随时间变化的图像如图所示，则下列结论错误的是( ) 
A．摩托车比汽车晚到 |
B．两地的路程为 |
C．摩托车的速度为 |
D．汽车的速度为 |
如图，正比例函数y1与反比例函数y2相交于点E（﹣1，2），若y1＞y2＞0，则x的取值范围在数轴上表示正确的是（ ）
A． |
B． |
C． |
D． |
如图，点A的坐标为（6，0），点B为y轴的负半轴上的一个动点，分别以OB，AB为直角边在第三、第四象限作等腰Rt△OBF，等腰Rt△ABE，连接EF交y轴于P点，当点B在y轴上移动时，PB的长度为（ ）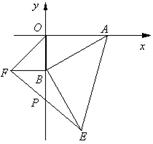
| A．2 | B．3 |
| C．4 | D．PB的长度随点B的运动而变化 |
如图，已知抛物线
，直线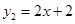
，当x任取一值时，x对应的函数值分别为y1、y2．若y1≠y2，取y1、y2中的较小值记为M；若y1=y2，记M=y1=y2．例如：当x=1时，y1=0，y2=4，y1＜y2，此时M=0．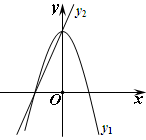
下列给出四个说法：
①当x＞0时，y1<y2；
②当x＜0时，x值越大，M值越大；
③使得M大于2的x值不存在；
④使得M=1的x值是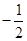
或
.
说法正确的个数是
| A．1个 | B．2个 | C．3个 | D．4个 |
梅凯种子公司以一定价格销售“黄金1号”玉米种子，如果一次购买10千克以上（不含10千克）的种子，超过10千克的那部分种子的价格将打折，并依此得到付款金额y（单位：元）与一次购买种子数量x（单位：千克）之间的函数关系如图所示，下列四种说法：
①一次购买种子数量不超过10千克时，销售价格为5元/千克；
②一次购买30千克种子时，付款金额为100元；
③一次购买10千克以上种子时，超过10千克的那部分种子的价格打五折；
④一次购买40千克种子比分两次购买且每次购买20千克种子少花25元钱．
其中正确的个数是（ ）
| A．1个 | B．2个 | C．3个 | D．4个 |
若ab＞0，则一次函数y=ax+b与反比例函数y=
在同一坐标系数中的大致图象是（ ）
A． |
B． |
C． |
D． |
粤公网安备 44130202000953号
，正方形除去圆部分的面积为
（阴影部分），则