初中数学一次函数的最值选择题

小亮家与学校相距1500m，一天放学后他步行回家，最初以某一速度匀速前进，途中遇到熟人小强，说话耽误了几分钟，与小强告别后他就改为匀速慢跑，最后回答了家，设小亮从学校出发后所用的时间为t（min），与家的距离为s（m），下列图象中，能表示上述过程的是（      ）

A．	B．
C．	D．

设min{x，y}表示x，y两个数中的最小值，例如min{1，2}=1，min{7，5}=5，则关于x的一次函数y=min{2x，x+1}可以表示为（     ）

A．y="2x"	B．y=x+1
C．	D．

如图所示．有下列说法：
①起跑后1小时内，甲在乙的前面；
②第1小时两人都跑了10千米；
③甲比乙先到达终点；
④两人都跑了20千米．其中正确的说法有（     ）

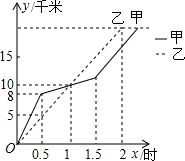
A．1个

B．2个

C．3个

D．4个

一次函数y=kx﹣k（k≠0）的图象如图所示，若y＞0，则x的取值范围是（ ）

A．x＜0

B．x＞0

C．x＞2

D．x＜2

“黄金1号”玉米种子的价格为5元/千克，如果一次购买2千克以上的种子，超过2千克部分的种子价格打6折，设购买种子数量为x千克，付款金额为y元，则y与x的函数关系的图象大致是（  ）

A．

B．

C．

D．

某人匀速跑步到公园，在公园里某处停留了一段时间，再沿原路匀速步行回家，此人离家的距离y与时间x的关系的大致图象是（ ）

A．	B．
C．	D．

如图，直线y₁=x+b与x轴、y轴分别交于A，B两点，与反比例函数y₂=-（x＜0）交于C，D两点，点C的横坐标为-1，过点C作CE⊥y轴于点E，过点D作DF⊥x轴于点F．下列说法：①b=6；②BC=AD；③五边形CDFOE的面积为35；④当x＜-2时，y₁＞y₂，其中正确的有（ ）

A．1个

B．2个

C．3个

D．4个

如图是石家庄某小区高层住户2014年的取暖费统计表，小宇家住1201（12楼）室，小鹏家住3301（33楼）室，小宇家和小鹏家的面积是一样的，该小区对28楼以上的住户的取暖费有优惠政策，在实施该政策以后，小宇发现小鹏家平均每平方米的取暖费比他家的少4.4元，则小宇家每平方米的取暖费为（ ）

A．21元

B．22元

C．23元

D．24元

抛物线y=ax²+bx+c图象如图所示，则一次函数y=-bx-4ac+b²与反比例函数y=在同一坐标系内的图象大致为（   ）

小亮从家步行到公交站台，等公交去学校，图中的折线表示小亮的行程s（千米）与所花时间t（分钟）之间的函数关系．下列说法错误的是（   ）

A．小亮行程8千米，共用了30分钟

B．小亮等公交车时间为6分钟

C．小亮步行的速度是100米/分钟

D．公交车的速度是350米/分钟

如图，已知直线y=-x+2与x轴交于点B，与y轴交于点A．过线段AB的中点A₁做A₁B₁⊥x轴于点B₁，过线段A₁B的中点A₂作A₂B₂⊥x轴于点B₂，过线段A₂B的中点A₃作A₃B₃⊥x轴于点B₃…，以此类推，则△A_nB_nB_n-1的面积为（   ）

A．      B．           C．              D．

已知等腰三角形的周长为20cm，将底边长y（cm）表示成腰长x（cm）的函数解析式为，则其自变量x的取值范围是（ ）

A．0＜x＜10

B．5＜x＜10

C．一切实数

D．x＞0

二次函数的图象如图所示，那么一次函数的图象大致是（ ）

A．

B．

C．

D．

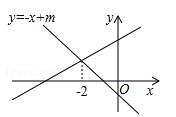
如图，直线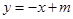与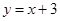的交点的横坐标为﹣2，则关于x的不等式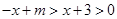的取值范围为（ ）

A．x＞﹣2

B．x＜﹣2

C．﹣3＜x＜﹣2

D．﹣3＜x＜﹣1

如图，在等腰△ABC中，AB=AC=4cm，∠B=30°，点P从点B出发，以cm/s的速度沿BC方向运动到点C停止，同时点Q从点B出发，以1cm/s的速度沿BA-AC方向运动到点C停止，若△BPQ的面积为y（cm²），运动时间为x（s），则下列最能反映y与x之间函数关系的图象是（     ）