初中数学一次函数的最值选择题

关于的函数和在同一坐标系中的图像大致是（   ）

一次函数与反比例函数的图像在同一直角坐标系下的大致图像如图所示，则k、b的取值范围是（    ）

A．

B．

C．

D．

从3，4，5这三个数中任取两个，分别记作p和q（p≠q），构造函数y=px－2和y=x+q，使这两个函数图象交点的横坐标始终小于2，则这样的有序数组（p，q）共有（   ）．

A．2对

B．3对

C．4对

D．5对

线段，当的值由增加到2时，该线段运动所经过的平面区域的面积为（   ）

A．6

B．8

C．9

D．10

教室里的饮水机接通电源就进入自动程序，开机加热时每分钟上升10℃，加热到100℃，停止加热，水温开始下降，此时水温（℃）与开机后用时（min）成反比例关系．直至水温降至30℃，饮水机关机．饮水机关机后即刻自动开机，重复上述自动程序．若在水温为30℃时，接通电源后，水温y（℃）和时间（min）的关系如图，为了在上午第一节下课时（8：45）能喝到不超过50℃的水，则接通电源的时间可以是当天上午的（　  ）

A．7：20

B．7：30

C．7：45

D．7：50

给出下列命题及函数，和的图象
①如果，那么；
②如果，那么；
③如果，那么；
④如果时，那么.
则（     ）

A．正确的命题是①④	B．错误的命题是②③④
C．正确的命题是①②	D．错误的命题只有③

图中给出的直线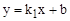和反比例函数的图像，判断下列结论正确的个数有（    ）
①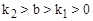；②直线 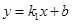与坐标轴围成的△ABO的面积是4；③方程组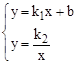的解为， ；④当－6＜x＜2时，有＞ .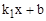

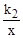A．1个

B．2个

C．3个

D．4个

如图，梯形ABCD中，AB∥DC，DE⊥AB，CF⊥AB，且AE=EF=FB=5，DE=12,动点P从点A出发，沿折线AD-DC-CB以每秒1个单位长的速度运动到点B停止.设运动时间为t秒，y=S_△EPF，则y与t的函数图象大致是(     )

如图，在x轴上有五个点，它们的横坐标依次为1，2，3，4，5．分别过这些点作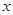轴的垂线与三条直线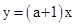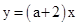，，相交，其中．则图中阴影部分的面积是（ 　　）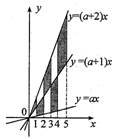

A．12.5

B．25

C．12.5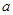

D．25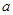

2013年“中国好声音”全国巡演重庆站在奥体中心举行．童童从家出发前往观看，先匀速步行至轻轨车站，等了一会儿，童童搭乘轻轨至奥体中心观看演出，演出结束后，童童搭乘邻居刘叔叔的车顺利回到家．其中x表示童童从家出发后所用时间，y表示童童离家的距离．下面能反映y与x的函数关系的大致图象是（　　）

A．

B．

C．

D．

如图，是一对变量满足的函数关系的图象，有下列3个不同的问题情境：
①小明骑车以400米/分的速度匀速骑了5分，在原地休息了4分，然后以500米/分的速度匀速骑回出发地，设时间为x分，离出发地的距离为y千米；
②有一个容积为6升的开口空桶，小亮以1.2升/分的速度匀速向这个空桶注水，注5分后停止，等4分后，再以2升/分的速度匀速倒空桶中的水，设时间为x分，桶内的水量为y升；
③矩形ABCD中，AB=4，BC=3，动点P从点A出发，依次沿对角线AC、边CD、边DA运动至点A停止，设点P的运动路程为x，当点P与点A不重合时，y=S_△ABP；当点P与点A重合时，y=0．
其中，符合图中所示函数关系的问题情境的个数为

A．0       B．1      C．2       D．3

对于点A（x₁，y₁），B（x₂，y₂），定义一种运算：．例如，A（－5，4），B（2，﹣3），．若互不重合的四点C，D，E，F，满足，则C，D，E，F四点【   】

A．在同一条直线上	B．在同一条抛物线上
C．在同一反比例函数图象上	D．是同一个正方形的四个顶点

甲、乙两辆摩托车同时从相距20km的A，B两地出发，相向而行．图中l₁，l₂分别表示甲、乙两辆摩托车到A地的距离s（km）与行驶时间t（h）的函数关系．则下列说法错误的是

A．乙摩托车的速度较快

B．经过0.3小时甲摩托车行驶到A，B两地的中点

C．经过0.25小时两摩托车相遇

D．当乙摩托车到达A地时，甲摩托车距离A地km

把直线向上平移m个单位后，与直线的交点在第一象限，则m的取值范围是

A．1＜m＜7

B．3＜m＜4

C．m＞1

D．m＜4

已知函数的图象如图所示，则一元二次方程根的存在情况是

A．没有实数根	B．有两个相等的实数根
C．有两个不相等的实数根	D．无法确定