[青海]2013年初中毕业升学考试(青海西宁卷)数学
使两个直角三角形全等的条件是
| A.一锐角对应相等 | B.两锐角对应相等 |
| C.一条边对应相等 | D.两条边对应相等 |
已知函数 的图象如图所示,则一元二次方程
的图象如图所示,则一元二次方程 根的存在情况是
根的存在情况是
| A.没有实数根 | B.有两个相等的实数根 |
| C.有两个不相等的实数根 | D.无法确定 |
如图,已知OP平分∠AOB,∠AOB= ,CP
,CP ,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是
,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是
A. |
B. |
C. |
D. |
如图,矩形的长和宽分别是4和3,等腰三角形的底和高分别是3和4,如果此三角形的底和矩形的宽重合,并且沿矩形两条宽的中点所在的直线自右向左匀速运动至等腰三角形的底与另一宽重合.设矩形与等腰三角形重叠部分(阴影部分)的面积为y,重叠部分图形的高为x,那么y关于x的函数图象大致应为
A. |
B. |
C. |
D. |
2013年青洽会已梳理15类302个项目总投资达363 000 000 000元. 将363 000 000 000元用科学记数法表示为 元.
张明想给单位打电话,可电话号码中的一个数字记不清楚了,只记得6352□87,张明在□的位置上随意选了一个数字补上,恰好是单位电话号码的概率是 .
如图,甲乙两幢楼之间的距离是30米,自甲楼顶A处测得乙楼顶端C处的仰角为 ,测得乙楼底部D处的俯角为
,测得乙楼底部D处的俯角为 ,则乙楼的高度为 米.
,则乙楼的高度为 米.
如图,是两块完全一样的含 角的三角板,分别记作△ABC和△A1B1C1,现将两块三角板重叠在一起,设较长直角边的中点为M,绕中点M转动上面的三角板ABC,使其直角顶点C恰好落在三角板A1B1C1的斜边A1B1上.当∠A
角的三角板,分别记作△ABC和△A1B1C1,现将两块三角板重叠在一起,设较长直角边的中点为M,绕中点M转动上面的三角板ABC,使其直角顶点C恰好落在三角板A1B1C1的斜边A1B1上.当∠A 30°,AC
30°,AC 10时,则此时两直角顶点C、C1的距离是 .
10时,则此时两直角顶点C、C1的距离是 .
如图,在平面直角坐标系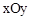 中,直线AB与
中,直线AB与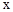 轴交于点A,与
轴交于点A,与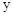 轴交于点C(
轴交于点C(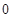 ,
,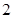 ),且与反比例 函数
),且与反比例 函数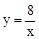 在第一象限内的图象交于点B,且BD⊥
在第一象限内的图象交于点B,且BD⊥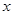 轴于点D,OD
轴于点D,OD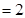 .
.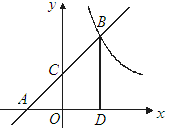
(1)求直线AB的函数解析式;
(2)设点P是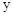 轴上的点,若△PBC的面积等于
轴上的点,若△PBC的面积等于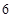 ,直接写出点P的坐标.
,直接写出点P的坐标.
在折纸这种传统手工艺术中,蕴含许多数学思想,我们可以通过折纸得到一些特殊图形.把一张正方形纸片按照图①~④的过程折叠后展开.
① ② ③ ④
(1)猜想四边形ABCD是什么四边形;
(2)请证明你所得到的数学猜想.
今年西宁市高中招生体育考试测试管理系统的运行,将测试完进行换算统分改为计算机自动生成,现场公布成绩,降低了误差,提高了透明度,保证了公平.考前张老师为了解全市初三男生考试项目的选择情况(每人限选一项),对全市部分初三男生进行了调查,将调查结果分成五类:A、实心球( kg);B、立定跳远;C、50米跑;D、半场运球;E、其它.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
kg);B、立定跳远;C、50米跑;D、半场运球;E、其它.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:

(1)将上面的条形统计图补充完整;
(2)假定全市初三毕业学生中有5500名男生,试估计全市初三男生中选50米跑的人数有多少人?
(3)甲、乙两名初三男生在上述选择率较高的三个项目:B、立定跳远;C、50米跑;D、半场运球中各选一项,同时选择半场运球、立定跳远的概率是多少?请用列表法或画树形图的方法加以说明并列出所有等可能的结果.
如图,⊙O是△ABC的外接圆,BC为⊙O直径,作∠CAD=∠B,且点D在BC的延长线上,CE⊥AD于点E.
(1)求证:AD是⊙O的切线;
(2)若⊙O的半径为8,CE=2,求CD的长.
青海新闻网讯:西宁市为加大向国家环境保护模范城市大步迈进的步伐,积极推进城市绿地、主题公园、休闲场地建设.园林局利用甲种花卉和乙种花卉搭配成A、B两种园艺造型摆放在夏都大道两侧.搭配数量如下表所示:
| |
甲种花卉(盆) |
乙种花卉(盆) |
| A种园艺造型(个) |
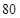 盆 盆 |
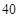 盆 盆 |
| B种园艺造型(个) |
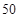 盆 盆 |
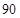 盆 盆 |
(1)已知搭配一个A种园艺造型和一个B种园艺造型共需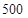 元.若园林局搭配A种园艺造型
元.若园林局搭配A种园艺造型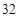 个,B种园艺造型
个,B种园艺造型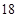 个共投入
个共投入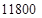 元.则A、B两种园艺 造型的单价分别是多少元?
元.则A、B两种园艺 造型的单价分别是多少元?
(2)如果搭配A、B两种园艺造型共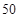 个,某校学生课外小组承接了搭配方案的设计,其中甲种花卉不超过
个,某校学生课外小组承接了搭配方案的设计,其中甲种花卉不超过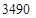 盆,乙种花卉不超过
盆,乙种花卉不超过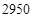 盆,问符合题意的搭配方案有几种?请你帮忙设计出来.
盆,问符合题意的搭配方案有几种?请你帮忙设计出来.
如图,正方形AOCB在平面直角坐标系 中,点O为原点,点B在反比例函数
中,点O为原点,点B在反比例函数 (
( >
> )图象上,△BOC的面积为
)图象上,△BOC的面积为 .
.
(1)求反比例函数 的关系式;
的关系式;
(2)若动点E从A开始沿AB向B以每秒1个单位的速度运动,同时动点F 从B开始沿BC向C以每秒 个单位的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动.若运动时间用t表示,△BEF的面积用
个单位的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动.若运动时间用t表示,△BEF的面积用 表示,求出S关于t的函数关系式,并求出当运动时间t取何值时,△BEF的面积最大?
表示,求出S关于t的函数关系式,并求出当运动时间t取何值时,△BEF的面积最大?
(3)当运动时间为 秒时,在坐标轴上是否存在点P,使△PEF的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
秒时,在坐标轴上是否存在点P,使△PEF的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
 的值是
的值是




 (
( >
> )
) =
=








 ,大圆半径是小圆半径的
,大圆半径是小圆半径的 倍,则小圆半径为
倍,则小圆半径为 或
或
 = .
= . 、
、 的方程组
的方程组 中,
中, .
.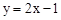 沿
沿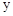 轴平移3个单位,则平移后直线与
轴平移3个单位,则平移后直线与 ,则弧AB的弧长
,则弧AB的弧长 .
. 
 ,且AE:BE =1:3,则AB= .
,且AE:BE =1:3,则AB= .

 ,然后在不等式
,然后在不等式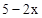 >
>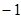 的非负整数解中选一个使原式有意义的数代入求值.
的非负整数解中选一个使原式有意义的数代入求值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号