[江苏]2013-2014学年江苏南京树人国际八年级上期末模拟数学试卷
在3.14、 、
、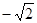 、
、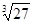 、
、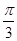 、0.2020020002这六个数中,无理数有( )
、0.2020020002这六个数中,无理数有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
如果点P(m,1-2m)在第一象限,那么m的取值范围是( )
A.0<m< |
B.- <m<0 <m<0 |
C.m<0 | D.m> |
已知函数 ,当x=1或3时,对应的两个函数值相等,则实数b的值是( )
,当x=1或3时,对应的两个函数值相等,则实数b的值是( )
| A.1 | B.-1 | C.2 | D.-2 |
已知等腰三角形的一个内角等于50º,则该三角形的一个底角的余角是( )
| A.25º | B.40º或30º | C.25º或40º | D.50º |
在边长为2的正三角形ABC中,已知点P是三角形内任意一点,则点P到三角形的三边距离之和PD+PE+PF等于( )
A. |
B.2 |
C.4 |
D.无法确定 |
如果 ,
, ,则函数
,则函数 的图象一定不经过( )
的图象一定不经过( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
从3,4,5这三个数中任取两个,分别记作p和q(p≠q),构造函数y=px-2和y=x+q,使这两个函数图象交点的横坐标始终小于2,则这样的有序数组(p,q)共有( ).
| A.2对 | B.3对 | C.4对 | D.5对 |
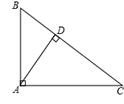
如图,在△ABC中,∠BAC=90º,AB=15,AC=20,AD⊥BC,垂足为D,则△ABC斜边上的高AD= .
下表给出的是关于某个一次函数的自变量x及其对应的函数值y的若干信息. 请你根据表格中的相关数据计算:m+2n= .
如图,△ABC是边长为a的等边三角形,D是BC边的中点,过点D分别作AB、AC的垂线,垂足为E、F.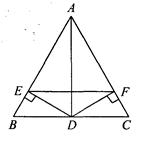
(1)计算:AD= ,EF= (用含a的式子表示);
(2)求证:DE=DF.
已知一次函数y=(1 2m)x+m+1,求当m为何值时.
2m)x+m+1,求当m为何值时.
(1)y随x的增大而增大?
(2)图象经过第一、二、四象限?
(3)图象经过第二、四象限?
(4)图象与y轴的交点在x轴的下方?
已知,如图所示,折叠长方形OABC的一边BC,使点B落在OA边的点D处,如果AB=8,BC=10,求E的坐标.
已知一次函数y=kx+b与y=mx+n的图象如图所示.
(1)写出关于x,y的方程组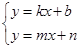 的解;
的解;
(2)若0<kx+b<mx+n,根据图像写出x的取值范围.
如图,直线y=-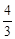 x+8与x轴、y轴分别相交于点A、B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B'处.
x+8与x轴、y轴分别相交于点A、B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B'处.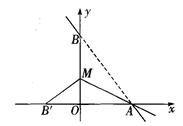
求: (1)点B'的坐标: .
(2)直线AM所对应的函数关系式.
某租赁公司共有50台联合收割机,其中甲型20台,乙型30台.现将这50台联合收割机派往A、B两地收割小麦,其中30台派往A地,20台派往B地.两地区与该租赁公司商定的每天的租赁价格如下:
| |
甲型收割机的租金 |
乙型收割机的租金 |
| A地 |
1800元/台 |
1600元/台 |
| B地 |
1600元/台 |
1200元/台 |
(1)设派往A地x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),请用x表示y,并注明x的范围.
(2)若使租赁公司这50台联合收割机一天获得的租金总额不低于79600元,说明有多少种分派方案,并将各种方案写出.
在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(小时)之间的关系如图所示,请根据图象所提供的信息解答下列问题: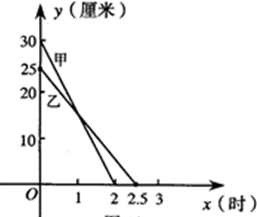
(1)甲、乙两根蜡烛燃烧前的高度分别是 , 从点燃到燃尽所用的时间分别 。
(2)分别求甲、乙两根蜡烛燃烧时y与x之间的函数关系式;
(3)燃烧多长时间时,甲、乙两根蜡烛的高度相等(不考虑都燃尽时的情况)?在什么事件段内,甲蜡烛比乙蜡烛高?在什么时间段内,甲蜡烛比乙蜡烛低?


 是一次函数,则k= .
是一次函数,则k= . 中自变量x的取值范围是 .
中自变量x的取值范围是 . 中,∠C=90°,∠ABC=60°,BD平分∠ABC,若AD=6,则CD= .
中,∠C=90°,∠ABC=60°,BD平分∠ABC,若AD=6,则CD= .
 的图象上,则实数a= .
的图象上,则实数a= .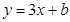 和
和 的图像交于点P(-2,-5),则根据图像可得不等式
的图像交于点P(-2,-5),则根据图像可得不等式 的解集是 .
的解集是 .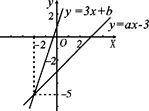

 的图象与y轴交于点A,一次函数
的图象与y轴交于点A,一次函数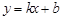 的图象 经过点B(0,-1),并且与x轴以及
的图象 经过点B(0,-1),并且与x轴以及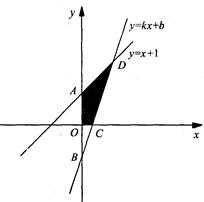
 粤公网安备 44130202000953号
粤公网安备 44130202000953号