如图,已知直线l:y= x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…;按此作法继续下去,则点A4的坐标为( )
x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…;按此作法继续下去,则点A4的坐标为( )
| A.(0,64) | B.(0,128) | C.(0,256) | D.(0,512) |
如图,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为 ,则a的值是( )
,则a的值是( )
A. |
B. |
C. |
D. |
如图,点A的坐标为(-1,0),点B在直线y=2x-4上运动,当线段AB最短时,点B的坐标是( )
A.(- ,- ,- ) ) |
B.( , , ) ) |
C.(- , , ) ) |
D.( ,- ,- ) ) |
甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息,已知甲先出发2秒,在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是 ( )
| A.①②③ | B.仅有①② |
| C.仅有①③ | D.仅有②③ |
如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2,例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:
①当x>0时,y1>y2;
②当x<0时,x值越大,M值越小;
③使得M大于2的x值不存在;
④使得M=1的x值是- 或
或 .
.
其中正确的是
| A.①② | B.①④ | C.②③ | D.③④ |
已知二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=bx+c和反比例函数y= 在同一平面直角坐标系中的图象大致是( ).
在同一平面直角坐标系中的图象大致是( ).

如图,直线y=kx+b经过点A(﹣1,﹣2)和点B(﹣2,0),直线y=2x过点A,则不等式2x<kx+b<0的解集为( )
| A.x<﹣2 | B.﹣2<x<﹣1 | C.﹣2<x<0 | D.﹣1<x<0 |
如图,爷爷从家(点O)出发,沿着扇形AOB上 的路径去匀速散步.设爷爷距家(点O)的距离为s,散步的时间为t,则下列图形中能大致刻画s与t之间函数关系的图象是( )
若ab>0,则一次函数y=ax+b与反比例函数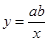 在同一坐标系数中的大致图象是( )
在同一坐标系数中的大致图象是( )
A  B
B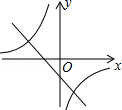 C
C  D
D 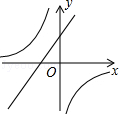
如图,梯形ABCD中,AD∥BC,BF⊥AD,CE⊥AD,且AF=EF=ED=5,BF=12,动点G从点A出发,沿折现AB-BC-CD以每秒1个单位长的速度运动到点D停止. 设运动时间为t秒,△EFG的面积为y,则y关于t的函数图像大致是( )

已知一次函数y=
 +m和y=
+m和y=
 +n的图象都经过点A(-2,0),且与y轴分别交于B、C两点,那么△ABC的面积是( )
+n的图象都经过点A(-2,0),且与y轴分别交于B、C两点,那么△ABC的面积是( )
A.2 B.3 C.4 D.6