[山东]2013年初中毕业升学考试(山东泰安卷)数学
2012年我国国民生产总值约52万亿元人民币,用科学记数法表示2012年我国国民生产总值为
| A.5.2×1012元 | B.52×1012元 | C.0.52×1014元 | D.5.2×1013元 |
实验学校九年级一班十名同学定点投篮测试,每人投篮六次,投中的次数统计如下:5,4,3,5,5,2,5,3,4,1,则这组数据的中位数,众数分别为
| A.4,5 | B.5,4 | C.4,4 | D.5,5 |
如图,五边形ABCDE中,AB∥CD,∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角,则∠1+∠2+∠3等于
A.90° B.180° C.210° D.270°
如图,点A,B,C,在⊙O上,∠ABO=32°,∠ACO=38°,则∠BOC等于
| A.60° | B.70° | C.120° | D.140° |
对于抛物线 ,下列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(-1,3);④x>1时,y随x的增大而减小,其中正确结论的个数为
,下列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(-1,3);④x>1时,y随x的增大而减小,其中正确结论的个数为
| A.1 | B.2 | C.3 | D.4 |
在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知在AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2,则P2点的坐标为
| A.(1.4,-1) | B.(1.5,2) | C.(1.6,1) | D.(2.4,1) |
有三张正面分别写有数字-1,1,2的卡片,它们背面完全相同,现将这三张卡片背面朝上洗匀后随机抽取一张,以其正面数字作为a的值,然后再从剩余的两张卡片随机抽一张,以其正面的数字作为b的值,则点(a,b)在第二象限的概率为
A. |
B. |
C. |
D. |
如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是 的中点,则下列结论不成立的是
的中点,则下列结论不成立的是
| A.OC∥AE | B.EC=BC | C.∠DAE=∠ABE | D.AC⊥OE |
某电子元件厂准备生产4600个电子元件,甲车间独立生产了一半后,由于要尽快投入市场,乙车间也加入该电子元件的生产,若乙车间每天生产的电子元件是甲车间的1.3倍,结果用33天完成任务,问甲车间每天生产电子元件多少个?在这个问题中设甲车间每天生产电子元件x个,根据题意可得方程为
A. |
B. |
C. |
D. |
把直线 向上平移m个单位后,与直线
向上平移m个单位后,与直线 的交点在第一象限,则m的取值范围是
的交点在第一象限,则m的取值范围是
| A.1<m<7 | B.3<m<4 | C.m>1 | D.m<4 |
如图,AB,CD是⊙O的两条互相垂直的直径,点O1,O2,O3,O4分别是OA、OB、OC、OD的中点,若⊙O的半径为2,则阴影部分的面积为
A.8 B.4 C.4π+4 D.4π-4
如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的边长为
A. |
B. |
C.4 | D.8 |
观察下列等式:
31=3,32=9,33=27,34=81,35=243,36=729,37=2187…
解答下列问题:3+32+33+34…+32013的末位数字是
| A.0 | B.1 | C.3 | D.7 |
如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,DE=1,则BE的长是 .
如图,某海监船向正西方向航行,在A处望见一艘正在作业渔船D在南偏西45°方向,海监船航行到B处时望见渔船D在南偏东45°方向,又航行了半小时到达C处,望见渔船D在南偏东60°方向,若海监船的速度为50海里/小时,则A,B之间的距离为 (取 ,结果精确到0.1海里).
,结果精确到0.1海里).
如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数
的图象经过点C,一次函数
的图象经过点
,一次函数
的图象经过点
,

(1)求反比例函数与一次函数的解析式;
(2)求点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,求P点的坐标.
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,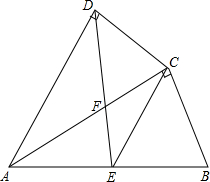
(1)求证:AC2=AB•AD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求 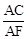 的值.
的值.
某商店购进600个旅游纪念品,进价为每个6元,第一周以每个10元的价格售出200个,第二周若按每个10元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低1元,可多售出50个,但售价不得低于进价),单价降低x元销售销售一周后,商店对剩余旅游纪念品清仓处理,以每个4元的价格全部售出,如果这批旅游纪念品共获利1250元,问第二周每个旅游纪念品的销售价格为多少元?
如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.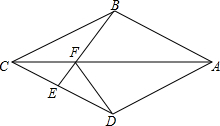
(1)证明:∠BAC=∠DAC,∠AFD=∠CFE;
(2)若AB∥CD,试证明四边形ABCD是菱形;
(3)在(2)的条件下,试确定E点的位置,∠EFD=∠BCD,并说明理由.
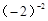 等于
等于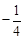
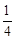









 的解集为
的解集为 的结果是
的结果是

 与二次函数
与二次函数 的图象可能是
的图象可能是



 .
.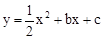 与y轴交于点C(0,-4),与x轴交于点A,B,且B点的坐标为(2,0)
与y轴交于点C(0,-4),与x轴交于点A,B,且B点的坐标为(2,0)
 粤公网安备 44130202000953号
粤公网安备 44130202000953号