如图,在平面直角坐标系中,点 在直线
在直线 上.连结
上.连结 将线段
将线段 绕点
绕点 顺时针旋转
顺时针旋转 ,点
,点 的对应点
的对应点 恰好落在直线
恰好落在直线 上,则
上,则 的值为( )
的值为( )
A. |
B. |
C. |
D. |
对于一次函数y=-x+4,下列结论错误)的是( )
| A.函数值随自变量的增大而减小 |
| B.点(4-a,a)在该函数的图象上 |
| C.函数的图象与直线y=x+2垂直 |
D.函数的图象与坐标轴围成的三角形的周长是4+4 |
正比例函数y=kx(k≠0)的图象在第二、四象限,则一次函数y=x+k的图象大致是( )
在▭ABCD中,对角线AC=4,BD=6,P是线段BD上一动点,过P作EF∥AC,与▱ABCD的两边分别交于E、F.设BP=x,EF=y,则反映y与x之间关系的图象是( )
二次函数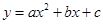 的图象如下图所示,则反比例函数
的图象如下图所示,则反比例函数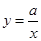 与一次函数
与一次函数 在同一坐标系中的大致图象是( )
在同一坐标系中的大致图象是( )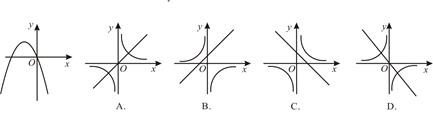
小亮家与姥姥家相距24km,小亮8:00从家出发,骑自行车去姥姥家.妈妈8:30从家出发,乘车沿相同路线去姥姥家.在同一直角坐标系中,小亮和妈妈的行进路程S(km)与北京时间t(时)的函数图象如图所示.根据图象得到小亮结论,其中错误的是( )
| A.小亮骑自行车的平均速度是12km/h |
| B.妈妈比小亮提前0.5小时到达姥姥家 |
| C.妈妈在距家12km处追上小亮 |
| D.9:30妈妈追上小亮 |
如图,在平面直角坐标系中,A(-3,1),以点O为直角顶点作等腰直角三角形AOB,双曲线 在第一象限内的图象经过点B,设直线AB的解析式为
在第一象限内的图象经过点B,设直线AB的解析式为 ,当
,当 时,
时, 的取值范围是( ).
的取值范围是( ).
A. |
B. 或 或 |
C. |
D. 或 或 |
某油箱容量为60 L的汽车,加满汽油后行驶了100 Km时,油箱中的汽油大约消耗了 ,如果加满汽油后汽车行驶的路程为x Km,邮箱中剩油量为y L,则y与x之间的函数解析式和自变量取值范围分别是( )
,如果加满汽油后汽车行驶的路程为x Km,邮箱中剩油量为y L,则y与x之间的函数解析式和自变量取值范围分别是( )
| A.y=0.12x,x>0 | B.y=60﹣0.12x,x>0 | C.y=0.12x,0≤x≤500 | D.y=60﹣0.12x,0≤x≤500 |
一次函数y=(m—1)x+m2的图象过点(0,4),且y随x的增大而增大,则m的值为( ).
| A.-2 | B.2 | C.1 | D.-2或2 |
如图,已知抛物线 和直线
和直线 。我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M= y1=y2。
。我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M= y1=y2。
下列判断:
①当x>2时,M=y2;
②当x<0时,x值越大,M值越大;
③使得M大于4的x值不存在;
④若M=2,则x=" 1" 。
其中正确的有 ( )
| A.1个 | B.2个 | C.3个 | D.4个 |
将2×2的正方形网格如图放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,正方形ABCD的顶点都在格点上.若直线y=kx(k≠0)与正方形ABCD有公共点,则k的取值范围是( )
| A.k≤2 | B.k≥ |
C. ≤k≤2 ≤k≤2 |
D. <k<2 <k<2 |
如图1,点E为矩形ABCD边AD上一点,点P,点Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s.设P,Q出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系的图象如图2(曲线OM为抛物线的一部分).则下列结论:
①AD=BE=5cm;
②当0<t≤5时, ;
;
③直线NH的解析式为 ;
;
④若△ABE与△QBP相似,则 秒.
秒.
其中正确结论的个数为( )
| A.4 | B.3 | C.2 | D.1 |
定义:若抛物线的顶点与x轴的两个交点构成的三角形是直角三角形,则这种抛物线就称为:“美丽抛物线”.如图所示,直线l: 经过点M(0,
经过点M(0, ),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…Bn(n,yn) (n为正整数),依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…An+1(xn+1,0)(n为正整数).若x1=d(0<d<1),当d为( )时,这组抛物线中存在美丽抛物线.
),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…Bn(n,yn) (n为正整数),依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…An+1(xn+1,0)(n为正整数).若x1=d(0<d<1),当d为( )时,这组抛物线中存在美丽抛物线.
A. 或 或 |
B. 或 或 |
C. 或 或 |
D. |