初中数学一次函数的最值选择题

如图所示，函数和的图象相交于（－1，1），（2，2）两点．当时，x的取值范围是（   ）

A．x＜-1

B．-1＜x＜2

C．x＞2

D．x＜-1或x＞2

一次函数 $y=-x+a-3$（ $a$为常数）与反比例函数 $y=-\frac{4}{x}$的图象交于 $A$、 $B$两点，当 $A$、 $B$两点关于原点对称时 $a$的值是（      ）．

A．

0

B．

-3

C．

3

D．

4

如图，在等腰△ABC中，直线l垂直底边BC，现将直线l沿线段BC从B点匀速平移至C点，直线l与△ABC的边相交于E、F两点．设线段EF的长度为y，平移时间为t，则下图中能较好反映y与t的函数关系的图象是（ ）

A．

B．

C．

D．

已知函数，当时，y的取值范围是（   ）

A．

B．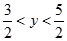

C．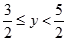

D．．

小明家、公交车站、学校在一条笔直的公路旁（小明家到这条公路的距离忽略不计）。一天，小明从家出发去上学，沿这条公路步行到公交车站恰好乘上一辆公交车，公交车沿这条路匀速行驶，小明下车时发现还有4分钟上课，于是他沿这条路跑步赶到学校（上、下车时间忽略不计），小明与家的距离s（单位：米）与他所用的时间t（单位：分钟）之间的函数关系如图所示。已知小明从家出发7分钟时与家的距离为1200米，从上车到他到达学校共用10分钟。下列说法：
①小明从家出发5分钟时乘上公交车  
②公交车的速度为400米/分钟
③小明下公交车后跑向学校的速度为100米/分钟  
④小明上课没有有迟到。
其中正确的个数是（ ）

A．1个

B．2个

C．3个

D．4个

在同一平面直角坐标系中，函数y=ax²+bx与y=bx+a的图象可能是（ ）

A．

B．

C．

D．

给出下列命题及函数y=x,y=x²和y=的图象，如图下列命题错误的是（   ）

A．如果0＜a＜1,那么＞a＞a^2

B．如果a＞1，那么a^2＞a＞；

C．如果－1＜a＜0，那么＞a^2＞a

D．如果a＜－1，那么a^2＞＞a；

小明骑自行车上学，开始以正常速度匀速行驶，但行至中途时，自行车出了故障，只好停下来修车，车修好后，因怕耽误上课，他比修车前加快了速度继续匀速行驶，下面是行驶路程s（m）关于时间t（min）的图象，那么符合小明行驶情况的大致图象是（   ）

如图，在矩形ABCD中，CD＝5，BC＝3，点P从起点A出发沿AD、DC向终点C匀速运动．设点P所走过的路程为x，点P所经过的线段与线段AB、BP所围成图形的面积为y．则在下列图像中，能正确反映y与x的函数关系的是 （ ）

李老师骑自行车上班，最初以某一速度匀速行进，中途由于自行车发生故障，停下修车耽误了几分钟，为了按时到校，李老师加快了速度，仍保持匀速行进，如果准时到校．在课堂上，李老师请学生画出他行进的路程y（千米）与行进时间t（小时）的函数图象的示意图，同学们画出的图象如图所示，你认为正确的是（     ）

已知实数a、b满足ab＞0，a+b＜0，则一次函数y=ax-b的图象可能是．

A．

B．

C．

D．

下列函数（1）y=3πx；（2）y=8x－6；（3）y=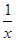；（4）y=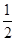－8x；（5）y=5x²－4x+1中，是一次函数的有

A．3个

B．4个

C．2个

D．1个

地铁1号线是重庆轨道交通线网东西方向的主干线，也是贯穿渝中区和沙坪坝区的重要交通通道，它的开通极大地方便了市民的出行。现某同学要从沙坪坝到两路口，他先匀速步行至沙坪坝地铁站，等了一会，然后搭乘一号线地铁直达两路口（忽略途中停靠站的时间）。在此过程中，他离沙坪坝的距离的函数关系的大致图象是（    ）

在平面直角坐标系内，函数y=x+3的图像与x轴、y轴分别交于A、B两点，点O为坐标原点，若在该坐标平面内有以点P（不与点A、B、O重合）为顶点的直角三角形与Rt△ABO全等，且这个以点P为顶点的直角三角形与Rt△ABO有一条公共边，则所有符合条件的P点个数为 （    ）
A．9个      B．7个      C．6个      D．5个

二次函数y=ax²+bx+c（a≠0）的图象如图所示，则函数y=与y=bx+c在同一直角坐标系内的大致图象是（ ）

A．

B．

C．

D．