山东省济南市历下区九年级4月教学质量检测(一模)数学试卷
如图,已知AB∥CD,∠A=70°,则∠1的度数是( ).
| A.70° | B.100° | C.110° | D.130° |
2014年,历下的教育惠民政策引起了社会的广泛关注,其中包括投入3600万元,免费为区属义务教育阶段中小学生提供校服.3600万元用科学记数表示为( ).
A. 元 元 |
B. 元 元 |
C. 元 元 |
D. 元 元 |
如图,一个几何体是由六个大小相同,棱长为1的立方块组成,则从上面看到的图形的面积是( ).
| A.6 | B.5 | C.4 | D.3 |
如图.在菱形ABCD中,对角线AC,BD交于点O,下列说法错误的是( ).
| A.AB∥DC | B.OA=OC | C.AC⊥BD | D.AC=BD |
一次函数y=(m—1)x+m2的图象过点(0,4),且y随x的增大而增大,则m的值为( ).
| A.-2 | B.2 | C.1 | D.-2或2 |
如图,AB是⊙O的直径,点C、D在⊙O上,若∠CAB=40°,则∠ADC的度数为( ).
A.25° B.30° C.45° D.50°
如图,在矩形ABCD中,AB=1,BC= .将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′ 的长度为( ).
.将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′ 的长度为( ).
A. |
B. |
C. +1 +1 |
D.2 |
如图,直线 与反比例函数
与反比例函数 (x>0)、
(x>0)、 (x>0)的图象分别交于B、C两点,A为y轴上任意一点,
(x>0)的图象分别交于B、C两点,A为y轴上任意一点, 的面积为3,则
的面积为3,则 的值为( ).
的值为( ).
A.2 B.3 C.4 D.5
某学习小组有6人,在一次数学测验中的成绩分别是:115,100,105,90,105,85,则他们成绩的极差和众数分别是( ).
| A.30和115 | B.30和105 | C.20和100 | D.15和105 |
如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,点M为边AB上的一动点,点N为边AC上的一动点,且∠MDN=90°,则cos∠DMN为( ).
A. |
B. |
C. |
D.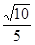 |
大家都知道,八点五十五可以说成九点差五分,有时这样表达更清楚.这启发人们设计了一种新的加减记数法.比如:9写成 ,
, ;198写成
;198写成 ,
, ;7683写成
;7683写成 ;
; ;总之,数字上画一杠表示减去它,按这个方法请计算
;总之,数字上画一杠表示减去它,按这个方法请计算 ( ).
( ).
| A.1990 | B.2068 | C.2134 | D.3024 |
二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论的个数是( ).
| A.1个 | B.2个 | C.3个 | D.4个 |
某班主任把本班学生上学方式的调查结果绘制成如图所示的不完整的统计图,已知骑自行车上学的学生有26人,则采用其他方式上学的学生人数为 人.
如图,在矩形ABCD中,AB=6cm,BC=8cm,E、F分别是BC、CD的中点,连接BF、DE,则图中阴影部分的面积是 cm2.
(本小题满分7分)
(1)如图,四边形ABCD、四边形AEFD是平行四边形.求证:△ABE≌△DCF.
(2)如图,CB是⊙O的直径,P是CB延长线上一点,PB=2,PA切⊙O于A点,PA=4.求⊙O的半径.
应用题分式方程(本小题满分8分)
我区某校九年级的同学利用清明假期外出踏青、赏春.从学校到景区共10千米,一部分同学骑自行车先出发,10分钟后,其余同学乘汽车出发,结果他们同时到达集合地点.已知汽车的速度是骑车同学速度的2倍,求两部分同学分别每小时走多少千米?
(本小题满分8分)为进一步弘扬祖国优秀传统文化,历下区教育局主办了“‘首善奖’历下区青少年书法大赛”.某校有2位同学获得一等奖,3位同学获得二等奖,随机抽取获奖同学谈谈他们的参赛体会.
(1)抽取一位同学谈体会,请直接写出该同学是二等奖获得者的概率;
(2)抽取两位同学谈体会,求两位同学分别是一等奖和二等奖获得者的概率.(用树状图或列表法求解)
(本小题满分9分)如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0,d)、C(-3,2).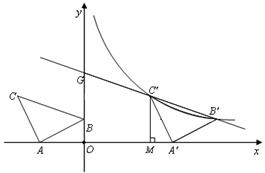
(1)求d的值;
(2)将△ABC沿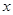 轴的正方向平移a个单位,在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图像上.请求出这个反比例函数和此时直线
轴的正方向平移a个单位,在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图像上.请求出这个反比例函数和此时直线 的解析式;
的解析式;
(3)在(2)的条件下,直线 交y轴于点G,作
交y轴于点G,作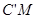 ⊥
⊥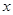 轴于
轴于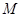 .
.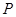 是线段
是线段 上的一点,若△
上的一点,若△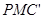 和△
和△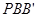 面积相等,求点
面积相等,求点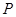 坐标.
坐标.
(本小题满分9分)在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.
(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;
(2)如图2,连接AA1,CC1.若△ABA1的面积为4,求△CBC1的面积;
(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1,求线段EP1长度的最大值与最小值.
(本小题满分9分)如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(1, 0)、C(3, 0)、D(3, 4).以A为顶点的抛物线y=ax2+bx+c过点C.动点P从点A出发,以每秒 个单位的速度沿线段AD向点D运动,运动时间为t秒.过点P作PE⊥x轴交抛物线于点M,交AC于点N.
个单位的速度沿线段AD向点D运动,运动时间为t秒.过点P作PE⊥x轴交抛物线于点M,交AC于点N.

(1)直接写出点A的坐标,并求出抛物线的解析式;
(2)当t为何值时,△ACM的面积最大?最大值为多少?
(3)点Q从点C出发,以每秒1个单位的速度沿线段CD向点D运动,当t为何值时,在线段PE上存在点H,使以C、Q、N、H为顶点的四边形为菱形?


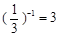
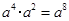

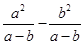 的结果是( ).
的结果是( ). = .
= .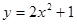 的图象上,则
的图象上,则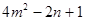 = .
= .
 ;
; .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号