初中数学一次函数的最值选择题

如图，点A的坐标为（-1，0）点B（a，a），当线段AB最短时，点B的坐标为（    ）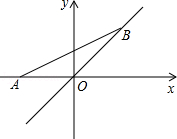

A．（0，0）

B．（，-）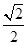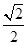

C．（-，-）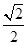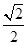

D．（-，-）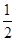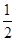

如图，在直角坐标系中，直线与坐标轴交于A、B两点，与双曲线（）交于点C，过点C作CD⊥x轴，垂足为D，且OA=AD，则以下结论：
①；
②当0＜x＜3时，；
③如图，当x=3时，EF=；
④当x＞0时，随x的增大而增大，随x的增大而减小．
其中正确结论的个数是（ ）

A．1      B．2      C．3      D．4

一家电信公司提供两种手机的月通话收费方式供用户选择，其中一种有月租费，另一种无月租费．这两种收费方式的通话费用y（元）与通话时间x（分钟）之间的函数关系如图所示．小红根据图象得出下列结论：
①l₁描述的是无月租费的收费方式；
②l₂描述的是有月租费的收费方式；
③当每月的通话时间为500分钟时，选择有月租费的收费方式省钱．
其中，正确结论的个数是（ ）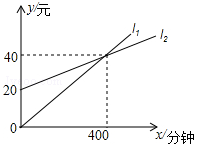

A．0

B．1

C．2

D．3

直线沿y轴向下平移6个单位后与x轴的交点坐标是（ ）

A．（﹣4，0）

B．（﹣1，0）

C．（0，2）

D．（2，0）

已知点A（﹣2，0），B为直线x=﹣1上一个动点，P为直线AB与双曲线的交点，且AP=2AB，则满足条件的点P的个数是（ ）

A．0个

B．1个

C．2个

D．3个

若关于x的一元二次方程有两个不相等的实数根，则一次函数的大致图象可能是（ ）

A．

B．

C．

D．

如图1，在矩形MNPQ中，动点R从点N出发，沿N→P→Q→M方向运动至点M处停止．设点R运动的路程为x，△MNR的面积为y，如果y关于x的函数图象如图2所示，则当x=9时，点R应运动到（   ）

A．M处

B．N处

C．P处

D．Q处

若函数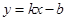的图象如图所示，则关于x的不等式的解集为（ ）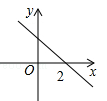

A．x＜2

B．x＞2

C．x＜5

D．x＞5

在平面直角坐标系中，点P（x，0）是x轴上一动点，它与坐标原点O的距离为y，则y关于x的函数图象大致是（ ）．

A．

B．

C．

D．

甲、乙两人在操场上赛跑，他们赛跑的路程S（米）与时间t（分钟）之间的函数关系如图所示，则下列说法错误的是（ ）

A．甲、乙两人进行1000米赛跑

B．甲先慢后快，乙先快后慢

C．比赛到2分钟时，甲、乙两人跑过的路程相等

D．甲先到达终点

若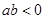，则正比例函数与反比例函数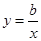在同一坐标系的大致图象可能是（ ）

A．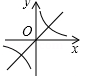

B．

C．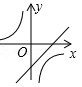

D．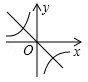

已知函数，当x=2时，函数值y为（ ）

A．5

B．6

C．7

D．8

如图，已知直线y₁=x+a与y₂=kx+b相交于点P（﹣1，2），则关于x的不等式x+a＞kx+b的解集正确的是（ ）

A．x＞1

B．x＞﹣1

C．x＜1

D．x＜﹣1

一次函数y=2x﹣6的图象经过（  ）

A．第一、二、三象限

B．第一、三、四象限

C．第一、二、四象限

D．第二、三、四象限

将直线y=﹣2x+1向下平移4个单位得到直线l，则直线l的解析式为（  ）

A．y=﹣6x+1

B．y=﹣2x﹣3

C．y=﹣2x+5

D．y=2x﹣3