将抛物线y=2x2向左平移3个单位,再向上平移1个单位得到的抛物线表达式是( ).
A.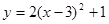 |
B.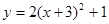 |
C.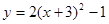 |
D.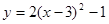 |
下列函数中,不是二次函数的是( )
A.y=l-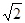 x2 x2 |
B.y= (x—1) (x+4) (x—1) (x+4) |
| C.y=2(x—1)2+4 |
| D.y=(x-2) 2-x2 |
对于抛物线y=- (x-5)2+3,下列判断中正确的是( )
(x-5)2+3,下列判断中正确的是( )
| A.开口向下,顶点坐标(5,3) |
| B.开口向上,顶点坐标(5,3) |
| C.开口向下,顶点坐示(-5,3) |
| D.开口向上,顶点坐示(-5,3) |
学生校服原来每套的售价是100元,后经连续两次降价,现在的售价是81元,则平均每次降价的百分数是 ( )
| A.9% | B.8.5% | C.9. 5% | D.10% |
抛物线 的顶点坐标是( )
的顶点坐标是( )
| A.(-2,-3) | B.(2,3) | C.(-2,3) | D.(2,-3) |
对于二次函数 ,有下列说法:
,有下列说法:
①如果当x≤1时 随
随 的增大而减小,则m≥1;
的增大而减小,则m≥1;
②如果它的图象与x轴的两交点的距离是4,则 ;
;
③如果将它的图象向左平移3个单位后的函数的最小值是-4,则m=-1;
④如果当x=1时的函数值与x=2013时的函数值相等,则当x=2014时的函数值为-3.
其中正确的说法是 .
如图,抛物线 与x轴交于点A、B两点,与y轴交于点C,且A点坐标(-3,0),连接BC、AC.
与x轴交于点A、B两点,与y轴交于点C,且A点坐标(-3,0),连接BC、AC.
(1)求该抛物线解析式;
(2)求AB和OC的长;
(3)点E从点B出发,沿x轴向点A运动(点E与点A、B不重合),过点E作直线l平行AC,交BC于点D,设BE的长为m,△BDE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(4)在(3)的条件下,连接CE,求△CDE面积的最大值.
若抛物线y=ax2经过P(1,﹣2),则它也经过 ( )
| A.(2,1) | B.(﹣1,2) | C.(1,2) | D.(﹣1,﹣2) |
已知函数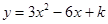 (
(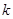 为常数)的图象经过点A(0.8,
为常数)的图象经过点A(0.8,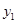 ),B(1.1,
),B(1.1,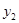 ),
),
C(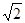 ,
,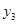 ),则有( )
),则有( )
A.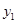 < <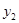 < <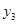 |
B.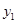 > >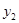 > >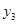 |
C.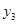 > >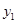 > >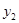 |
D.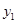 > >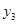 > >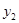 |