初中数学二次函数在给定区间上的最值试题

如果二次函数y＝ax²+bx+c（a≠0）的图象如图所示，那么（   ）

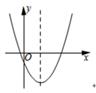
A．a＜0，b＞0，c＞0

B．a＞0，b＜0，c＞0

C．a＞0，b＞0，c＜0

D．a＞0，b＜0，c＜0

抛物线的对称轴是（ ）

A．直线

B．直线

C．直线

D．直线

已知抛物线y=ax²+bx+c与x轴的公共点是（﹣4，0），（2，0），则这条抛物线的对称轴是直线　_________　．

下列函数，一定是二次函数的是（    ）

A．y=x^2-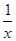

B．y=ax^2+bx+c

C．y=（x-3）^2-x^2

D．y=（m^2+1）x^2（m为常数）

判断下列哪一组的a、b、c，可使二次函数y=ax²+bx+c﹣5x²﹣3x+7在坐标平面上的图形有最低点（   ）

A．a=0，b=4，c=8	B．a=2，b=4，c=-8
C．a=4，b=-4，c=8	D．a=6，b=-4，c=-8

从-3，-2，-1，0，1，2这六个数中，任意抽取一个数，作为反比例函数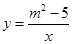和二次函数y=（m+1）x²+mx+1中的m的值，恰好使所得的反比例函数在每个象限内，y随x的增大而增大，且二次函数的图象开口向上的概率为                     ．

二次函数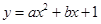（a≠0）的图象的顶点在第一象限，且过点（﹣1，0）．设t=a+b+1，则t值的变化范围是（   ）

A．0＜t＜1

B．0＜t＜2

C． 1＜t＜2

D．﹣1＜t＜1

抛物线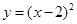的顶点坐标是（   ）

A．（0，－2）

B．（－2，0）

C．（0，2）

D．（2，0）

如图，是二次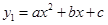函数和一次函数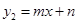的图象，观察图象写出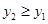时，x的取值范围__________．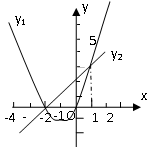

若把二次函数y=x²+6x+2化为y=（x-h）²+k的形式，其中h，k为常数，则h+k=         ．

已知二次函数y=ax²+bx+c的图象如图，其对称轴x=﹣1，给出下列结果：
①b²＞4ac；②abc＞0；③2a+b=0；④a+b+c＞0；⑤a﹣b+c＜0，
则正确的结论是（ ）

A．①②③④

B．②④⑤

C．②③④

D．①④⑤

已知函数y=
（1）若这个函数是一次函数，求m的值;
（2）若这个函数是二次函数，则m的值应怎样？

若抛物线y=ax²经过P（1，﹣2），则它也经过 (     )

A．（2，1）

B．（﹣1，2）

C．（1，2）

D．（﹣1，﹣2）

（本题8分）抛物线上部分点的横坐标x，纵坐标y的对应值如下表：

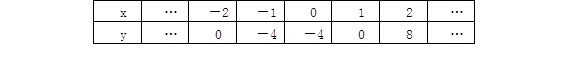
（1）根据上表填空：
① 抛物线与x轴的交点坐标是          和          ；
② 抛物线经过点 （-3，       ）；
③ 在对称轴右侧，y随x增大而        ；
（2）试确定抛物线的解析式．

已知二次函数的图象如图所示，有以下结论：
①abc＞0，
②a﹣b+c＜0，
③2a=b，
④4a+2b+c＞0，
⑤若点（﹣2，）和（，）在该图象上，则．
其中正确的结论是      （填入正确结论的序号）．