初中数学二次函数在给定区间上的最值解答题

如图，已知直线y=-x+3与x轴、y轴分别交于A，B两点，抛物线y=-x²+bx+c经过A，B两点，点P在线段OA上，从点O出发，向点A以1个单位/秒的速度匀速运动；同时，点Q在线段AB上，从点A出发，向点B以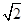个单位/秒的速度匀速运动，连接PQ，设运动时间为t秒．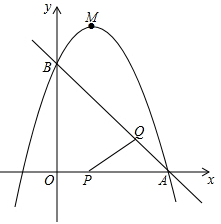

（1）求抛物线的解析式；
（2）问：当t为何值时，△APQ为直角三角形；
（3）过点P作PE∥y轴，交AB于点E，过点Q作QF∥y轴，交抛物线于点F，连接EF，当EF∥PQ时，求点F的坐标；
（4）设抛物线顶点为M，连接BP，BM，MQ，问：是否存在t的值，使以B，Q，M为顶点的三角形与以O，B，P为顶点的三角形相似？若存在，请求出t的值；若不存在，请说明理由．

如图1，把边长分别是为4和2的两个正方形纸片OABC和OD′E′F′叠放在一起．
（1）操作1：固定正方形OABC，将正方形OD′E′F′绕点O按顺时针方向旋转45°得到正方形ODEF，如图2，连接AD、CF，线段AD与CF之间有怎样的数量关系？试证明你的结论；
（2）操作2，如图2，将正方形ODEF沿着射线DB以每秒1个单位的速度平移，平移后的正方形ODEF设为正方形PQMN，如图3，设正方形PQMN移动的时间为x秒，正方形PQMN与正方形OABC的重叠部分面积为y，直接写出y与x之间的函数解析式；
（3）操作3：固定正方形OABC，将正方形OD′E′F′绕点O按顺时针方向旋转90°得到正方形OHKL，如图4，求△ACK的面积．

如图，二次函数y=ax²＋2ax＋b的图象与x轴交于点A、B，与y轴交于点C（0，），其顶点在直线y=－2x上.
（1）求a，b的值；
（2）写出当－2≤x≤2时，二次函数y的取值范围；
（3）以AC、CB为一组邻边作□ACBD，则点D关于x轴的对称点D’是否在该二次函数的图象上？请说明理由.

如图，抛物线与x轴交于两点，直线与y 轴交于点，与轴交于点,点是轴上方的抛物线上一动点，过点作轴于点，交直线于点.设点的横坐标为。

（1）求抛物线的解析式；
（2）若,求的值；
（3）若点是点关于直线的对称点、是否存在点，使点落在y轴上？若存在，求出相应的点的坐标；若不存在，请说明理由。

（本小题满分12分）如图， 在直角坐标系xOy中,一次函数y=－x+m（m为常数）的图像与x轴交于A(-3,0)，与y轴交于点C。以直线x=－1为对称轴的抛物线y=a+bx+c(a,b,c为常数，且a＞0)经过A，C两点，与x轴正半轴交于点B.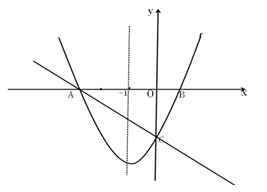

(1)求一次函数及抛物线的函数表达式。
(2)已知在对称轴上是否存在一点P,使得PBC的周长最小，若存在，请求出点P的坐标.
(3)点D是线段OC上的一个动点（不与点O、点C重合），过点D作DE‖PC交x轴于点E,连接PD、PE。设CD的长为m, △PDE的面积为S。求S与m之间的函数关系式。并说明S是否存在最大值，若存在，请求出最大值：若不存在，请说明理由。

如图所示，在平面直角坐标系xOy中，矩形OABC的边长OA、OC分别为12cm、6cm，点A、C分别在y轴的负半轴和x轴的正半轴上，抛物线y=ax²+bx+c经过点A、B，且18a+c=0．

（1）求抛物线的解析式．
（2）如果点P由点A开始沿AB边以1cm/s的速度向终点B移动，同时点Q由点B开始沿BC边以2cm/s的速度向终点C移动．
①移动开始后第t秒时，设△PBQ的面积为S，试写出S与t之间的函数关系式，并写出t的取值范围．
②当S取得最大值时，在抛物线上是否存在点R，使得以P、B、Q、R为顶点的四边形是平行四边形？如果存在，求出R点的坐标；如果不存在，请说明理由．

（本小题满分9分）某电子厂商投产一种新型电子厂品，每件制造成本为18元，试销过程中发现，每月销售量y（万件）与销售单价x（元）之间的关系可以近似地看作一次函数y=－2x+100．（利润=售价﹣制造成本）
(1)写出每月的利润z（万元）与销售单价x（元）之间的函数关系式；
(2)当销售单价为多少元时，厂商每月能获得350万元的利润？当销售单价为多少元时，厂商每月能获得最大利润？最大利润是多少？
(3)根据相关部门规定，这种电子产品的销售单价不能高于32元，如果厂商要获得每月不低于350万元的利润，那么制造出这种产品每月的最低制造成本需要多少万元？

（本小题满分5分）已知反比例函数y＝的图象与二次函数y＝ax²＋x－1的图象相交于点A（2，2）

（1）求反比例函数与二次函数的解析式；
（2）设二次函数图象的顶点为B，判断点B是否在反比例函数的图象上，并说明理由；

（3）若反比例函数图象上有一点P，点P的横坐标为1，求△AOP的面积．

已知直线与茹、轴分别相交于B，A两点，抛物线过A，B两点，且对称轴为直线．

（1）求A，B两点的坐标，并求抛物线的解析式；
（2）若点P以1个单位/秒的速度从点B沿轴向点O运动．过点P作轴的平行线交直线AB于点M，交抛物线于点N．设点P运动的时间为，MN的长度为S，求S与之间的函数关系式，并求出当为何值时，S取得最大值?
（3）设抛物线的对称轴CD与直线AB相交于点D，顶点为C．问：在（2）条件不变情况下，是否存在一个值，使四边形CDMN是平行四边形?若存在，求出的值；若不存在，请说明理由．

如图，在矩形ABCD中，AB=3，AD=4，P是BC上的任意一点（P与B、C不重合），过点P作AP⊥PE，垂足为P，PE交CD于点E．

（1）连接AE，当△APE与≌△ADE时，求BP的长；
（2）设BP=x，CE=y，确定y与x的函数关系式；
（3） 当x取何值时，AE的长最短，求x的值和AE的长．

如图，在平面直角坐标系xOy中，A、B为x轴上两点，C、D为y轴上的两点，经过点A、C、B的抛物线的一部分C₁与经过点A、D、B的抛物线的一部分C₂组成一条封闭曲线，我们把这条封闭曲线称为“蛋线”，已知点C的坐标为（0，-），点M是抛物线C₂：y=mx²-2mx-3m(m<0)的顶点.

（1）求A、B两点的坐标；
（2）“蛋线”在第四象限内是否存在一点P，使得∆PBC的面积最大？若存在，求出∆PBC面积的最大值；若不存在，请说明理由；
（3）当∆BDM为直角三角形时，请直接写出m的值.(参考公式：在平面直角坐标系中，若M(x₁,y₁)，N(x₂,y₂)，则M、N两点间的距离为MN=.

如图1，对于平面上小于等于90°的∠MON，我们给出如下定义：若点P在∠MON的内部或边上，作PE⊥OM于点E，PF⊥ON于点F，则将PE+PF称为点P与∠MON的“点角距”，记作d（∠MON，P）．如图2，在平面直角坐标系xOy中，x、y正半轴所组成的角为∠xOy．

（1）已知点A（5，0）、点B（3，2），则d（∠xOy，A）=       ，d（∠xOy，B）=          ．
（2）若点P为∠xOy内部或边上的动点，且满足d（∠xOy，P）=5，画出点P运动所形成的图形．
（3）如图3与图4，在平面直角坐标系xOy中，射线OT的函数关系式为y=x（x≥0）．
①在图3中，点C的坐标为（4，1），试求d（∠xOT，C）的值；
②在图4中，抛物线y=-x²+2x+经过A（5，0）与点D（3，4）两点，点Q是A，D两点之间的抛物线上的动点（点Q可与A，D两点重合），求当d（∠xOT，Q）取最大值时点Q 的坐标．

如图(1)，直线与x轴交于点A、与y轴交于点D，以AD为腰，以x轴为底作等腰梯形ABCD(AB＞CD)，且等腰梯形的面积是8，抛物线经过等腰梯形的四个顶点.

图(1)
(1) 求抛物线的解析式；
(2) 如图（2）若点P为BC上的—个动点（与B、C不重合），以P为圆心，BP长为半径作圆，与轴的另一个交点为E，作EF⊥AD，垂足为F，请判断EF与⊙P的位置关系，并给以证明；

图（2）
(3) 在（2）的条件下，是否存在点P，使⊙P与y轴相切，如果存在，请求出点P的坐标；如果不存在，请说明理由.

如图①，梯形ABCD中，AD∥BC，∠C=90°，BA=BC．动点E、F同时从点B出发，点E沿折线 BA-AD-DC运动到点C时停止运动，点F沿BC运动到点C时停止运动，它们运动时的速度都是1cm/s．设E出发t s时，△EBF的面积为y cm2．已知y与t的函数图象如图②所示，其中曲线OM为抛物线的一部分，MN、NP为线段．

请根据图中的信息，解答下列问题：
（1）AD=        cm，BC=       cm；
（2）求a的值，并用文字说明点N所表示的实际意义；
（3）直接写出当自变量t为何值时，函数y的值等于5．

【课本节选】
反比例函数y=（k为常数,k≠0）的图象是双曲线.当k＞0时，双曲线两个分支分别在三象限,在每一个象限内,y随x的增大而减小（简称增减性）；反比例函数的图象关于原点对称（简称对称性）．这些我们熟悉的性质，可以通过说理得到吗？
【尝试说理】
我们首先对反比例函数y=（k＞0）的增减性来进行说理．如图，当x＞0时．

在函数图象上任意取两点A、B，设A（x₁，），B（x₂，），
且0＜x₁＜x₂．
下面只需要比较和的大小．
—=．
∵0＜x₁＜x₂，∴x₁－x₂＜0，x₁ x₂＞0，且 k＞0．
∴＜0．即＜．
这说明：x₁＜x₂时，＞．也就是：自变量值增大了，对应的函数值反而变小了．
即：当x＞0时，y随x的增大而减小．
同理，当x＜0时，y随x的增大而减小．
（1）试说明：反比例函数y= （k＞0）的图象关于原点对称．
【运用推广】
（2）分别写出二次函数y=ax²（a＞0，a为常数）的对称性和增减性，并进行说理．
对称性：                                           ；
增减性：                                           ．
说理：

（3）对于二次函数y=ax²＋bx＋c （a＞0，a，b，c为常数），请你从增减性的角度，简要解释为何当x=—时函数取得最小值．