【课本节选】
反比例函数y=(k为常数,k≠0)的图象是双曲线.当k>0时,双曲线两个分支分别在三象限,在每一个象限内,y随x的增大而减小(简称增减性);反比例函数的图象关于原点对称(简称对称性).这些我们熟悉的性质,可以通过说理得到吗?
【尝试说理】
我们首先对反比例函数y=(k>0)的增减性来进行说理.如图,当x>0时.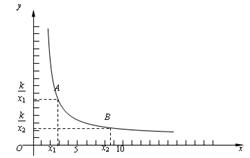
在函数图象上任意取两点A、B,设A(x1,),B(x2,),
且0<x1<x2.
下面只需要比较和的大小.
—=.
∵0<x1<x2,∴x1-x2<0,x1 x2>0,且 k>0.
∴<0.即<.
这说明:x1<x2时,>.也就是:自变量值增大了,对应的函数值反而变小了.
即:当x>0时,y随x的增大而减小.
同理,当x<0时,y随x的增大而减小.
(1)试说明:反比例函数y= (k>0)的图象关于原点对称.
【运用推广】
(2)分别写出二次函数y=ax2(a>0,a为常数)的对称性和增减性,并进行说理.
对称性: ;
增减性: .
说理:
(3)对于二次函数y=ax2+bx+c (a>0,a,b,c为常数),请你从增减性的角度,简要解释为何当x=—时函数取得最小值.
相关知识点
推荐套卷
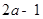 和
和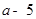 是一个正数m的两个平方根,则
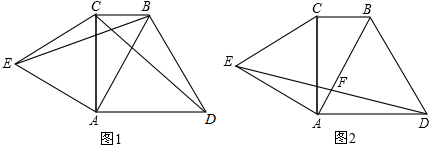
是一个正数m的两个平方根,则 ,m
,m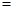 。
。

 粤公网安备 44130202000953号
粤公网安备 44130202000953号