如图,已知O是平面直角坐标系的原点,半径为1的⊙B经过点O,且与x、y
轴分别交于点A、C,点A的坐标为(-,0),AC的延长线与⊙B的切线OD
交于点D.
(1)求OC的长和∠CAO的度数;
(2)求点D的坐标;
(3)求过点A,O,D三点的抛物线的解析式;
(4)在(3)中,点P是抛物线上的一点,试确定点P的位置,使得△AOP的
面积与△AOC的面 积相等.
积相等.
心理学家通过实验发现:初中学生听讲的注意力随时间变化,讲课开始时,学生注意力逐渐增强,中间有一段平稳状态,随后开始分散.学生注意力指标数y随时间表t(分钟)变化的函数图象如下.当0≤t≤10时,图像是抛物线的一部分,当10≤t≤20时和20≤t≤40时,图像是线段。
(1)当0≤t≤10时,求注意力指标数y与时间t的函数关系式;
(2)一道数学探究题需要讲解24分钟,问老师能否经过恰当安排,使学生在探究这道题时,注意力指标数不低于45?请通过计算说明.
如图,抛物线 与
与 轴交于A、B两点,与y轴交于点
轴交于A、B两点,与y轴交于点
C(0,-1).且对称轴为 .
.
(1)求抛物线的解析式及A、B两点的坐标;
(2)点D在x轴下方的抛物线上,则四边形ABDC的面积是否存在最大值,若存在,求出此时点D的坐标;若不存在,请说明理由;
(3)点Q在y轴上,点P在抛物线上,要使Q、P、A、B为顶点的四边形是平行四边形,求出所有满足条件的点P的坐标.
某工厂生产的某种产品按质量分为10个档次,第1档次(最低档次)的产品一天能生产95件,每件利润6元.每提高一个档次,每件利润增加2元,但一天产量减少5件.(1)若生产第x档次的产品一天的总利润为y元(其中x为正整数,且1≤x≤10),求出y关于x的函数关系式;(2)若生产第x档次的产品一天的总利润为1120元,求该产品的质量档次.
如图1:矩形OABC的顶点A、B在抛物线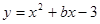 上,OC在
上,OC在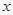 轴上,且
轴上,且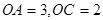 .
.
(1)求抛物线的解析式及抛物线的对称轴.
(2)如图2,边长为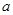 的正方形ABCD的边CD在
的正方形ABCD的边CD在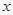 轴上,A、B两点在抛物线上,请用含
轴上,A、B两点在抛物线上,请用含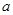 的代数式表示点B的坐标,并求出正方形边长
的代数式表示点B的坐标,并求出正方形边长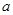 的值.
的值.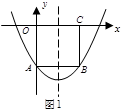
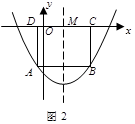
已知,等边△ABC边长为6,P为BC边上一点,且BP=4,点E、F分别在边AB、AC上,且∠EPF=60°,设BE=x,CF=y.
(1)求y与x的函数关系式,并写出x的取值范围;
(2)①若四边形AEPF的面积为 时,求x的值.
时,求x的值.
②四边形AEPF的面积是否存在最大值?若存在,请求出面积的最大值及此时x的值;若不存在,请说明理由.
已知:如图,在平面直角坐标系xOy中,直线 与x轴、y轴分别交于点A、B,点C在线段AB上,且
与x轴、y轴分别交于点A、B,点C在线段AB上,且 .
.
(1)求点C的坐标(用含有m的代数式表示);
(2)将△AOC沿x轴翻折,当点C的对应点C′恰好落在抛物线 上时,求该抛物线的表达式;
上时,求该抛物线的表达式;
(3)设点M为(2)中所求抛物线上一点,当以A、O、C、M为顶点的四边形为平行四边形时,请直接写出所有满足条件的点M的坐标.
如图,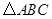 为直角三角形,
为直角三角形,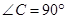 ,
,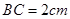 ,
,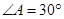 ;四边形
;四边形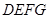 为矩形,
为矩形,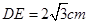 ,
,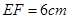 ,且点
,且点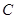 、
、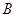 、
、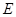 、
、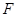 在同一条直线上,点
在同一条直线上,点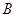 与点
与点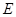 重合.
重合.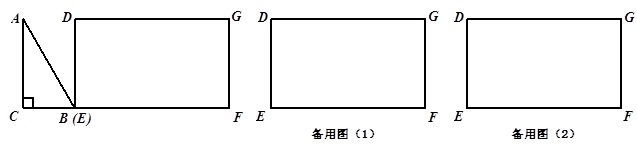
(1)求边
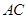 的长;
的长;(2)将
 以每秒
以每秒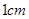 的速度沿矩形
的速度沿矩形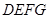 的边
的边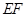 向右平移,当点
向右平移,当点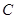 与点
与点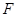 重合时停止移动,设
重合时停止移动,设 与矩形
与矩形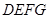 重叠部分的面积为
重叠部分的面积为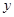 ,请求出重叠部分的面积
,请求出重叠部分的面积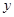 (
(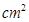 )与移动时间
)与移动时间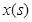 的函数关系式(时间不包含起始与终止时刻);
的函数关系式(时间不包含起始与终止时刻);(3)在(2)的基础上,当
 移动至重叠部分的面积为
移动至重叠部分的面积为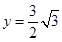
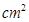 时,将
时,将 沿边
沿边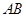 向上翻折,得到
向上翻折,得到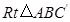 ,请求出
,请求出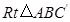 与矩形
与矩形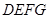 重叠部分的周长(可利用备用图).
重叠部分的周长(可利用备用图).
如图所示,已知点C(-3,m),点D(m-3,0).直线CD交y轴于点A.作CE与X轴垂直,垂足为E,以点B(-1,0)为顶点的抛物线恰好经过点A、C.

(1)则∠CDE= ;
(2)求抛物线对应的函数关系式;
(3)设P(x,y)为抛物线上一点(其中-3<x<1-或-1<x<1,连结BP并延长交直线CE于点N,记N点的纵坐标为yN,连结CP并延长交X轴于点M.
①试证明:EM•(EC+yN)为定值;
②试判断EM+EC+yN是否有最小值,并说明理由
如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(8,0)、(0,6).动点Q从点O、动点P从点A同时出发,分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤5).以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连接CD、QC.
(1)求当t为何值时,点Q与点D重合?
(2)设△QCD的面积为S,试求S与t之间的函数关系式,并求S的最大值;
(3)若⊙P与线段QC只有一个交点,请直接写出t的取值范围.
 如图,已知抛物线y=x2+bx+c与x轴交于A、B两点(A点在B点左侧),与y
如图,已知抛物线y=x2+bx+c与x轴交于A、B两点(A点在B点左侧),与y
轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.
⑴求抛物线的函数表达式;
⑵求直线BC的函数表达式;
⑶点E为y轴上一动点,CE的垂直平分线交CE于点F,交抛物线于P、Q两点,且点P在第三象限.
①当线段PQ=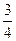 AB时
AB时 ,求tan∠CED的值;
,求tan∠CED的值;
②当以点C、D、E为顶点的三角形是直角三角形时,请直接写出点P的坐标.
温馨提示:考生可以根据第⑶问的题意,在图中补出图形,以便作答.
如图1,把边长分别是为4和2的两个正方形纸片OABC和OD′E′F′叠放在一起.
(1)操作1:固定正方形OABC,将正方形OD′E′F′绕点O按顺时针方向旋转45°得到正方形ODEF,如图2,连接AD、CF,线段AD与CF之间有怎样的数量关系?试证明你的结论;
(2)操作2,如图2,将正方形ODEF沿着射线DB以每秒1个单位的速度平移,平移后的正方形ODEF设为正方形PQMN,如图3,设正方形PQMN移动的时间为x秒,正方形PQMN与正方形OABC的重叠部分面积为y,直接写出y与x之间的函数解析式;
(3)操作3:固定正方形OABC,将正方形OD′E′F′绕点O按顺时针方向旋转90°得到正方形OHKL,如图4,求△ACK的面积.
如图,二次函数y=ax2+2ax+b的图象与x轴交于点A、B,与y轴交于点C(0,),其顶点在直线y=-2x上.
(1)求a,b的值;
(2)写出当-2≤x≤2时,二次函数y的取值范围;
(3)以AC、CB为一组邻边作□ACBD,则点D关于x轴的对称点D’是否在该二次函数的图象上?请说明理由.
一玩具厂去年生产某种玩具,成本为10元/件,出厂价为12元/件,年销售量
2万件.今年计划通过适当增加成本来提高产品档次,以拓展市场.若今年这种玩具每件的
成本比去年成本增加0.7x倍,今年这种玩具每件的出厂价比去年出厂价相应提高0.5x倍,
则预计今年年销售量将比去年年销售量增加x倍(本题中0<x≤11).
⑴用含x的代数式表示,今年生产的这种玩具每件的成本为________元,今年生产的这种玩具每件的出厂价为_________元.
⑵求今年这种玩具的每件利润y元与x之间的函数关系式.
⑶设今年这种玩具的年销售利润为w万元,求当x为何值时,今年的年销售利润最大?最大年销售利润是多少万元?
注:年销售利润=(每件玩具的出厂价-每件玩具的成本)×年销售量.
如图,抛物线 与x轴交于
与x轴交于 两点,直线
两点,直线 与y 轴交于点
与y 轴交于点 ,与
,与 轴交于点
轴交于点 ,点
,点 是
是 轴上方的抛物线上一动点,过点
轴上方的抛物线上一动点,过点 作
作 轴于点
轴于点 ,交直线
,交直线 于点
于点 .设点
.设点 的横坐标为
的横坐标为 。
。
(1)求抛物线的解析式;
(2)若 ,求
,求 的值;
的值;
(3)若点 是点
是点 关于直线
关于直线 的对称点、是否存在点
的对称点、是否存在点 ,使点
,使点 落在y轴上?若存在,求出相应的点
落在y轴上?若存在,求出相应的点 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。