在某节习题课上,老师在黑板上写下了关于x的二次函数y=kx2+(k+1)x+2-4k.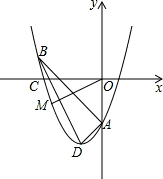
(1)某两位同学经过思考,对上述的二次函数进行了如下总结:
①该二次函数的图象经过点(1,3);
②当k<0时,该二次函数的图象与y轴的正半轴有交点;
请你判断上面两条结论是真命题还是假命题,并说明理由;
(2)若二次函数y=kx2+(k+1)x+2-4k的图象如图所示,该函数图象经过点B(-3,1)且与y轴交于点A,与x轴的负半轴交于点C,D为图象的顶点.
①求∠BAD的度数;
②点M在第三象限,且点M在二次函数图象上,连接OM.若∠ABD=∠MOC,求点M的横坐标.
已知抛物线C:y=-x2+bx+c经过A(-3,0)和B(0,3)两点,将这条抛物线的顶点记为M,它的对称轴与x轴的交点记为N.
(1)求抛物线C的表达式;
(2)求点M的坐标;
(3)将抛物线C平移到抛物线C′,抛物线C′的顶点记为M′,它的对称轴与x轴的交点记为N′.如果以点M、N、M′、N′为顶点的四边形是面积为16的平行四边形,那么应将抛物线C怎样平移?为什么?
在平面直角坐标系中,点A的坐标为(0,1),抛物线y=ax2+bx+c的顶点为坐标原点O,且与直线y=2x-4有唯一交点B.

(1)抛物线的函数表达式为 ;
(2)如图1,设直线y=2x-4与y轴交于点D,点P是抛物线上一点.
①过点P作PE∥y轴,交直线BD于点E,若△ADE与△ABD相似,求点P的坐标;
②将△ABD沿直线BD折叠后,点A落在点C处(图2),是否存在点P,使得S△PCD=3S△PAB?如果存在,请求出所有满足条件的点P的坐标;如果不存在,请说明理由.
如图,在平面直角坐标系中,抛物线y=-x2+bx+c与y轴交于点A(0,3),且经过点(5,-2),点B与点A关于对称轴对称,过点B作BC⊥x轴,垂足为C,连结OB.
(1)求二次函数的解析式,并求出点B的坐标.
(2)把△AOB以每秒1个单位的速度向右平移,得到△PDE,PE交OB于点F,PD交BC于点M,设向右平移运动的时间为t(s).设平移过程中与△OBC重叠部分的面积为S,试探求S 与t的函数关系式,并求当t为何值时,S最大?
(3)在(2)的条件下,是否存在某一时刻t,使△OCE为等腰三角形?若存在,求出t;若不存在,请说明理由.
如图,已知抛物线y=
 ﹣
﹣ x﹣2图象与x轴相交于A,B两点(点A在点B的左侧).若C(m,1﹣m)是抛物线上位于第四象限内的点,D是线段AB上的一个动点(不与A,B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.
x﹣2图象与x轴相交于A,B两点(点A在点B的左侧).若C(m,1﹣m)是抛物线上位于第四象限内的点,D是线段AB上的一个动点(不与A,B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.
(1)求点A和点B的坐标;
(2)求证:四边形DECF是矩形;
(3)连接EF,线段EF的长是否存在最小值?若存在,求出EF的最小值;若不存在,请说明理由.
如图,在平面直角坐标系中,抛物线y=a +bx﹣3(a≠0)与x轴交于点A(﹣2,0)、B(4,0)两点,与y轴交于点C.
+bx﹣3(a≠0)与x轴交于点A(﹣2,0)、B(4,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,当△PBQ存在时,求运动多少秒使△PBQ的面积最大,最大面积是多少?
(3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使S△CBK:S△PBQ=5:2,求K点坐标.
如图,抛物线y=(x+m)2+m,与直线y=﹣x相交于E,C两点(点E在点C的左边),抛物线与x轴交于A,B两点(点A在点B的左边).△ABC的外接圆⊙H与直线y=﹣x相交于点D.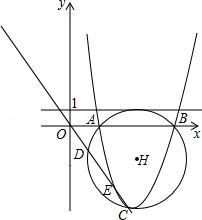
(1)若抛物线与y轴的交点坐标为(0,2),求m的值;
(2)求证:⊙H与直线y=1相切;
(3)若DE=2EC,求⊙H的半径.
如图,某建筑物的截面可以视作由两条线段AB,BC和一条曲线围成的封闭的平面图形.已知AB⊥BC,曲线是以点D为顶点的抛物线的一部分,BC=6m,点D到BC,AB的距离分别为4m和2m.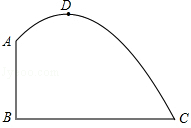
(1)请以BC所在直线为x轴(射线BC的方向为正方向),AB所在直线为y轴建立平面直角坐标系,求出抛物线的解析式,并直接写出自变量的取值范围;
(2)求AB的长.
如图,顶点为P(2,-4)的二次函数图象经过原点(0,0),点A在该图象上,OA交其对称轴l于点M,
(1)求该二次函数的关系式.
(2)若点A的坐标是(3,-3),求△OAP的面积.
(3)当点A在对称轴l右侧的二次函数图象上运动时,l上有一点N,且点M、N关于点P对称,试证明:∠ANM=∠ONM.
如图,在平面直角坐标系中,以A(3,0)为圆心,以5为半径的圆与x轴相交于B、C,与y轴的负半轴相交于D.
(1)若抛物线y=ax2+bx+c经过B、C、D三点,求此抛物线的解析式,并写出抛物线与圆A的另一个交点E的坐标;
(2)若动直线MN(MN∥x轴)从点D开始,以每秒1个长度单位的速度沿y轴的正方向移动,且与线段CD、y轴分别交于M、N两点,动点P同时从点C出发,在线段OC上以每秒2个长度单位的速度向原点O运动,连接PM,设运动时间为t秒,当t为何值时, 的值最大,并求出最大值;
的值最大,并求出最大值;
(3)在(2)的条件下,若以P、C、M为顶点的三角形与△OCD相似,求实数t的值.
研究所对某种新型产品的产销情况进行了研究,为投资商在甲、乙两地生产并销售该产品提供了如下成果:第一年的年产量为x(吨)时,所需的全部费用y(万元)与x满足关系式y= x2+5x+90,
x2+5x+90,
投入市场后当年能全部售出,且在甲、乙两地每吨的售价p甲、p乙(万元)均与x满足一次函数关系.(注:年利润=年销售额-全部费用)
(1)成果表明,在甲地生产并销售x吨时,p甲=- x+14,请你用含x的代数式表示甲地当年的年销售额,并求年利润W甲(万元)与x之间的函数关系式;
x+14,请你用含x的代数式表示甲地当年的年销售额,并求年利润W甲(万元)与x之间的函数关系式;
(2)成果表明,在乙地生产并销售x吨时,p乙=- x+n(n为常数),且在乙地当年的最大年利润为35万元.试确定n的值;
x+n(n为常数),且在乙地当年的最大年利润为35万元.试确定n的值;
(3)受资金、生产能力等多种因素的影响,某投资商计划第一年生产并销售该产品18吨,根据(1)、(2)中的结果,请你通过计算帮他决策,选择在甲地还是乙地产销才能获得最大的年利润?
已知点M,N的坐标分别为(0,1),(0,-1),点P是抛物线y= x2上的一个动点.
x2上的一个动点.
(1)求证:以点P为圆心,PM为半径的圆与直线y=-1的相切;
(2)设直线PM与抛物线y= x2的另一个交点为点Q,连接NP,NQ,求证:∠PNM=∠QNM.
x2的另一个交点为点Q,连接NP,NQ,求证:∠PNM=∠QNM.
如图,三角形ABC是以BC为底边的等腰三角形,点A、C分别是一次函数y=- x+3的图象与y轴、x轴的交点,点B在二次函数
x+3的图象与y轴、x轴的交点,点B在二次函数 的图象上,且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形.
的图象上,且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形.
(1)试求b,c的值,并写出该二次函数表达式;
(2)动点P从A到D,同时动点Q从C到A都以每秒1个单位的速度运动,问:
①当P运动到何处时,有PQ⊥AC?
②当P运动到何处时,四边形PDCQ的面积最小?此时四边形PDCQ的面积是多少?
综合与探究:如图,在平面直角坐标系xOy中,四边形OABC是平行四边形,A、C两点的坐标分别为(4,0),(-2,3),抛物线W经过O、A、C三点,D是抛物线W的顶点.
(1)求抛物线W的解析式及顶点D的坐标;
(2)将抛物线W和▱OABC一起先向右平移4个单位后,再向下平移m(0<m<3)个单位,得到抛物线W′和▱O′A′B′C′,在向下平移的过程中,设▱O′A′B′C′与▱OABC的重叠部分的面积为S,试探究:当m为何值时S有最大值,并求出S的最大值;
(3)在(2)的条件下,当S取最大值时,设此时抛物线W′的顶点为F,若点M是x轴上的动点,点N是抛物线W′上的动点,试判断是否存在这样的点M和点N,使得以D、F、M、N为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
如图1,抛物线y=- x2+bx+c与x轴相交于点A,C,与y轴相交于点B,连接AB,BC,点A的坐标为(2,0),tan∠BAO=2,以线段BC为直径作⊙M交AB于点D,过点B作直线l∥AC,与抛物线和⊙M的另一个交点分别是E,F.
x2+bx+c与x轴相交于点A,C,与y轴相交于点B,连接AB,BC,点A的坐标为(2,0),tan∠BAO=2,以线段BC为直径作⊙M交AB于点D,过点B作直线l∥AC,与抛物线和⊙M的另一个交点分别是E,F.
(1)求该抛物线的函数表达式;
(2)求点C的坐标和线段EF的长;
(3)如图2,连接CD并延长,交直线l于点N,点P,Q为射线NB上的两个动点(点P在点Q的右侧,且不与N重合),线段PQ与EF的长度相等,连接DP,CQ,四边形CDPQ的周长是否有最小值?若有,请求出此时点P的坐标并直接写出四边形CDPQ周长的最小值;若没有,请说明理由.