山西省阳泉市平定县九年级下学期中考一模数学试卷
如图,把一副三角尺叠放在一起,若AB∥CD,则∠1的度数是( )

| A.75° | B.60° | C.45° | D.30° |
已知一个布袋里装有2个红球,3个白球和a个黄球,这些球除颜色外其余都相同.若从该布袋里任意摸出1个球,是红球的概率为 ,则a等于( )
,则a等于( )
| A.1 | B.2 | C.3 | D.4 |
已知a是实数,则一元二次方程 +ax﹣4=0的根的情况是( )
+ax﹣4=0的根的情况是( )
| A.没有实数根 | B.有两个相等的实数根 |
| C.有两个不相等的实数根 | D.根据a的值来确定 |
2015年,县委、县政府做出了“小微企业富民,大中企业强县,唱响千年文化,建设美好平定”的决策,如图是小明制作的一个正方体的表面展开图,原正方体中与“建”字所在的面相对的面上标的字是( )

| A.美 | B.好 | C.平 | D.定 |
如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔60海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P的距离为( )

A.30 海里 海里 |
B.30 海里 海里 |
C.60海里 | D.30 海里 海里 |
一个正方形和四个全等的小正方形按图①②两种方式摆放,若把图②中未被小正方形覆盖部分(图②中的阴影部分)折成一个无盖的长方体盒子,则此长方体盒子的体积为( )

A. |
B. |
C. |
D. |
在平面直角坐标系中,已知点A(﹣4,2),B(﹣2,﹣2),以原点O为位似中心,相似比为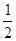 ,把△AOB缩小,则点A的对应点A′的坐标是( )
,把△AOB缩小,则点A的对应点A′的坐标是( )
| A.(﹣2,1) | B.(﹣8,4) |
| C.(﹣8,4)或(8,﹣4) | D.(﹣2,1)或(2,﹣1) |
在直角坐标系中,一直线l向下平移3个单位后所得直线b经过点A(0,3),将直线b绕点A顺时针旋转60°后所得直线经过点B(﹣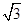 ,0),则直线l的函数关系式为( )
,0),则直线l的函数关系式为( )
A.y=﹣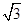 x x |
B.y=﹣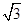 x+6 x+6 |
C.y=﹣ x x |
D.y=﹣ x+6 x+6 |
“智慧小组”有女生2人,男生3人,若从中随机选出两人参加小组展示学习活动,则选取的两人正好为一男一女的概率是 .
学校课外生物小组的试验园地是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道(如图),要使种植面积为600平方米,求小道的宽.若设小道的宽为x米,则可列方程为 .

如图,正方形ABCD的边长为2,点E是BC边的中点,过点B作BG⊥AE,垂足为G,延长BG交AC于点F,则CF= .

下面方格中有一个菱形ABCD和点O,请你在方格中画出以下图形(只要求画出平移、旋转后的图形,不要求写出作图步骤和过程).
(1)画出菱形ABCD向右平移6格后的四边形A1B1C1D1;
(2)画出菱形ABCD以点O为旋转中心,沿逆时针方向旋转90°后的四边形A2B2C2D2.
根据阳泉市教育局3月份通知,从2016年中考起,九年级学生信息技术考试成绩统计入中考总分,我县某中学为了提高八年级学生学习信息技术的积极性,组织了“信息技术技能竞赛”活动,八年级甲、乙两班根据初赛成绩,各选出5名选手参加复赛,这些选手的复赛成绩(满分为100分)如图所示:

(1)根据统计图填写下表:
班级 平均数 众数 方差
甲班 85 85
乙班 160
(2)根据上表可知,两个班选手成绩较稳定的是 ;
(3)选手小明说:“这次竞赛我得了80分,在我们班选手中成绩排名属下游!(后两名)”观察统计图,求出两班选手成绩的中位数,说明小明是哪个班的学生?
(4)学校要给其中一个班发集体优胜奖,你认为发给哪个班合适?请综合考评,说明理由.
如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,AE是⊙O的切线,∠CAE=60°.
(1)求∠D的度数;
(2)当BC=4时,求劣弧AC的长.
阅读材料:以下是我们教科书中的一段内容,请仔细阅读,并解答有关问题.
公元前3世纪,古希腊学家阿基米德发现:若杠杆上的两物体与支点的距离与其重量成反比,则杠杆平衡,后来人们把它归纳为“杠杆原理”,通俗地说,杠杆原理为:
阻力×阻力臂=动力×动力臂
【问题解决】
若工人师傅欲用撬棍动一块大石头,已知阻力和阻力臂不变,分别为1500N和0.4m.
(1)动力F(N)与动力臂l(m)有怎样的函数关系?当动力臂为1.5m时,撬动石头需要多大的力?
(2)若想使动力F(N)不超过题(1)中所用力的一半,则动力臂至少要加长多少?
【数学思考】
(3)请用数学知识解释:我们使用撬棍,当阻力与阻力臂一定时,为什么动力臂越长越省力.
【问题情境】一节数学课后,老师布置了一道课后练习题:
如图:已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,点E、F分别在A和BC上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF.
(1)阅读理解,完成解答
本题证明的思路可用下列框图表示:
根据上述思路,请你完整地书写这道练习题的证明过程;
(2)特殊位置,证明结论
若CE平分∠ACD,其余条件不变,求证:AE=BF;
(3)知识迁移,探究发现
如图,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上且满足EC=EF,请直接写出AE与BF的数量关系.(不必写解答过程)
 的相反数是( )
的相反数是( )
 •a=
•a= =4
=4 +
+
 b÷
b÷ b
b

 的解是 .
的解是 . ×
× ÷
÷ ﹣2sin30°﹣
﹣2sin30°﹣
 .
. .
.
 ﹣
﹣ x﹣2图象与x轴相交于A,B两点(点A在点B的左侧).若C(m,1﹣m)是抛物线上位于第四象限内的点,D是线段AB上的一个动点(不与A,B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.
x﹣2图象与x轴相交于A,B两点(点A在点B的左侧).若C(m,1﹣m)是抛物线上位于第四象限内的点,D是线段AB上的一个动点(不与A,B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号