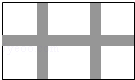
学校课外生物小组的试验园地是长35米、宽20米的矩形，为便于管理，现要在中间开辟一横两纵三条等宽的小道（如图），要使种植面积为600平方米，求小道的宽．若设小道的宽为x米，则可列方程为 ．
相关试题
相关知识点
推荐套卷
学校课外生物小组的试验园地是长35米、宽20米的矩形，为便于管理，现要在中间开辟一横两纵三条等宽的小道（如图），要使种植面积为600平方米，求小道的宽．若设小道的宽为x米，则可列方程为 ．
粤公网安备 44130202000953号