一个不透明的布袋里装有3个球,其中2个红球,1个白球,它们除颜色外其余都相同。
(1)求摸出1个球是白球的概率;
(2)摸出1个球,记下颜色后放回,并搅均,再摸出1个球。求两次摸出的球恰好颜色不同的概率(要求画树状图或列表);
(3)现再将n个白球放入布袋,搅均后,使摸出1个球是白球的概率为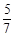 。求n的值。
。求n的值。
相关知识点
推荐套卷
一个不透明的布袋里装有3个球,其中2个红球,1个白球,它们除颜色外其余都相同。
(1)求摸出1个球是白球的概率;
(2)摸出1个球,记下颜色后放回,并搅均,再摸出1个球。求两次摸出的球恰好颜色不同的概率(要求画树状图或列表);
(3)现再将n个白球放入布袋,搅均后,使摸出1个球是白球的概率为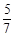 。求n的值。
。求n的值。