初中数学二次函数在给定区间上的最值选择题

抛物线y=（x-1）²+3的对称轴是（   ）

A．直线

B．直线

C．直线

D．直线

某幢建筑物，从10 m高的窗口A，用水管向外喷水，喷出的水流呈抛物线状(抛物线所在的平面与墙面垂直，如果抛物线的最高点M离墙1 m，离地面m，则水流落地点B离墙的距离OB是(   )

A．2 m

B．3 m

C．4 m

D．5 m

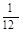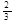如图，铅球运动员掷铅球的高度y(m)与水平距离x(m)之间的函数关系式是y=－x2+x+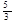，则该运动员此次掷铅球的成绩是(    )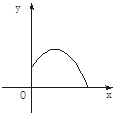

A．6 m

B．12 m

C．8 m

D．10 m

某乡镇企业现在年产值是15万元，如果每增加100元投资，一年增加250元产值，那么总产值y(万元)与新增加的投资额x(万元)之间函数关系为(   )

A．y=25x+15

B．y=2.5x+1.5

C．y=2.5x+15

D．y=25x+1.5

如图，一次函数y=－2x+3的图象与x、y轴分别相交于A、C两点，二次函数y=x2+bx+c的图象过点c且与一次函数在第二象限交于另一点B，若AC∶CB=1∶2，那么，这个二次函数的顶点坐标为(   )

A.(－，)         B.(－，)         C.(，)        D.(，－)

如果抛物线y=－x2+2(m－1)x+m+1与x轴交于A、B两点，且A点在x轴正半轴上，B点在x轴的负半轴上，则m的取值范围应是(   )
A.m>1              B.m>－1          C.m<－1            D.m<1

把一个小球以20 m/s的速度竖直向上弹出，它在空中的高度h(m)与时间t(s)满足关系h=20t－5t2.当h="20" m时，小球的运动时间为（  ）

A．20 s

B．2 s

C．(2+2) s

D．(2－2) s

为了备战2012英国伦敦奥运会，中国足球队在某次训练中，一队员在距离球门12米处的挑射，正好从2.4米高(球门横梁底侧高)入网.若足球运行的路线是抛物线y=ax2+bx+c(如图5所示)，则下列结论正确的是(   )

①a<－ ②－<a<0 ③a－b+c>0 ④0<b<－12a

A．①③

B．①④

C．②③

D．②④

无论m为任何实数，二次函数y=x2+(2－m)x+m的图象总过的点是(   )

A．(－1，0);

B．(1，0)

C．(－1，3) ;

D．(1，3)

二次函数y=x2－4x+3的图象交x轴于A、B两点，交y轴于点C，△ABC的面积为(   )
A.1               B.3               C.4              D.6

如图6所示，在一个直角三角形的内部作一个长方形ABCD，其中AB和BC分别在两直角边上，设AB="x" m，长方形的面积为y m2，要使长方形的面积最大，其边长x应为(  )

A． m

B．6 m

C．15 m

D． m

抛物线y=kx2－7x－7的图象和x轴有交点，则k的取值范围是(   )

A．k>－;

B．k≥－且k≠0;

C．k≥－;

D．k>－且k≠0

已知抛物线y=ax2+bx+c如图，则关于x的方程ax2+bx+c－8=0的根的情况是

A．有两个不相等的正实数根 ;	B．有两个异号实数根;
C．有两个相等的实数根 ;	D．没有实数根.

关于二次函数y=ax2+bx+c的图象有下列命题，其中是假命题的个数是（  ）
①当c=0时，函数的图象经过原点; ②当b=0时，函数的图象关于y轴对称;
③函数的图象最高点的纵坐标是;
④当c>0且函数的图象开口向下时，方程ax2+bx+c=0必有两个不相等的实根(    )

A．0个

B．1个

C．2个

D．3个

函数y=ax＋1与y=ax2＋bx＋1（a≠0）的图象可能是（   ）