初中数学二次函数在给定区间上的最值选择题

已知二次函数（a≠0）的图象如图所示，则下列结论：

① ac >0； ② a–b +c <0； ③当x <0时，y <0；
④方程（a≠0）有两个大于－1的实数根．
其中错误的结论有

A．② ③

B．② ④

C．① ③

D．① ④

二次函数的图象如图所示，则下列结论正确的是

A．

B．

C．

D．

二次函数y＝ax2＋bx＋c的图象如图所示，下列结论错误的是(    )

A．ab＜0

B．ac＜0

C．当x＜2时，函数值随x增大而增大；当x＞2时，函数值随x增大而减小

D．二次函数y＝ax2＋bx＋c的图象与x轴交点的横坐标就是方程ax2＋bx＋c＝0的根

二次函数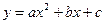的图象如图所示，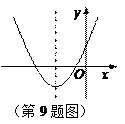

则一次函数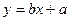的图象不经过

A．第一象限

B．第二象限

C．第三象限

D．第四象限

如图，点A，B的坐标分别为（1, 4）和（4, 4）,抛物线的顶点在线段AB上运动，与x轴交于C、D两点（C在D的左侧），点C的横坐标最小值为，则点D的横坐标最大值为(▲)

A．－3   　       B．1              C．5               D．8

y=x²＋（1－a）x＋1是关于x的二次函数，当x的取值范围是1≤x≤3时，y在x＝1时取得最大值，则实数a的取值范围是（   ）。

A．a=5

B．a≥5

C．a＝3

D．a≥3

坐标平面上，若移动二次函数y=2(x-175)(x-176)+6的图形，使其与x轴交于两点，且此两点的距离为1单位，则移动方式可为下列哪一种？

A．向上移动3单位

B．向下移动3单位

C．向上移勤6单位

D．向下移动6单位

坐标平面上有一函数y=24x²-48的图形，其顶点坐标为何？

A．(0，-2)

B．(1，-24)

C．(0，-48)

D．(2，48)

二次函数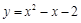的图象如图所示，

则函数值y＜0时x的取值范围是

A．x＜－1

B．x＞2

C．－1＜x＜2

D．x＜－1或x＞2

已知抛物线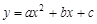的开口向下,顶点坐标为（2，－3） ,那么该抛物线有（  ▲ ）

A．最小值 －3

B．最大值－3

C．最小值2

D．最大值2

定义[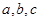]为函数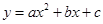的特征数, 下面给出特征数为 [2m，1 – m , –1– m]
的函数的一些结论：
① 当m =" –" 3时，函数图象的顶点坐标是(，)；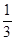
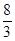② 当m > 0时，函数图象截x轴所得的线段长度大于；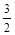
③ 当m < 0时，函数在x >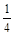时，y随x的增大而减小；
④ 当m¹ 0时，函数图象经过同一个点.
其中正确的结论有

A．①②③④

B．①②④

C．①③④

D．②④

如图，在矩形ABCD中， AB=4，BC=6，当直角三角板MPN 的直角顶点P在BC边上移动时，直角边MP始终经过点A，设直角三角板的另一直角边PN与CD相交于点Q．BP=x，CQ=y，那么y与x之间的函数图象大致是

如图5，

已知抛物线的对称轴为，点A，B均在抛物线上，且AB与x轴平行，其中点A的坐标为（0，3），则点B的坐标为

A．（2，3）

B．（3，2）

C．（3，3）

D．（4，3）

根据下表中的二次函数的自变量与函数的对应值，可判断该二次函数的图象与轴（   ）．

	…					…
	…					… A．只有一个交点 B．有两个交点，且它们分别在轴两侧 C．有两个交点，且它们均在轴同侧 D．无交点

如图2，从地面竖立向上抛出一个小球，小球的高度h（单位：m）与 小球运动时间t（单位：s）之间的关系式为h=30t-5t²，那么小球从抛出至回落到地面所需要的时间是（   ）．

A．6s

B．4s

C．3s

D．2s