初中数学二次函数在给定区间上的最值选择题

已知二次函数y=ax²+bx+c（a＜0）的图象如图所示，当-5≤x≤0时，下列说法正确的是（ ）

A．有最小值-5、最大值0

B．有最小值-3、最大值6

C．有最小值0、最大值6

D．有最小值2、最大值6

如图（1）是一个横断面为抛物线形状的拱桥，当水面在直线l时，拱顶（拱桥洞的最高点）离水面2m，水面宽4m．如图（2）建立平面直角坐标系，则抛物线的关系式是（ ）

A．y=－2

B．y=2

C．y=－

D．y=

一抛物线和抛物线y＝－2x²的形状、开口方向完全相同，顶点坐标是（－1，3），则该抛物线的解析式为（   ）

A．y＝－2（x－1）^2＋3

B．y＝－（2x＋1）^2＋3

C．y＝－2（x＋1）^2＋3

D．y＝－（2x－1）^2＋3

二次函数y=ax²+bx+c的顶点为D（－1,2）,与x轴的一个交点A在点（－3,0）和（－2,0）之间,其部分图象如图,则以下结论:

①b²－4ac<0;②a+b+c<0;③c－a=2;④方程ax²+bx+c－2=0有两个相等的实数根．其中正确结论的个数为（ ）．

A．1个

B．2个

C．3个

D．4个

抛物线y=3x ²，y= -3x ²，y=x ²+3共有的性质是（     ）．

A．

开口向上

B．

对称轴是y轴

C．

都有最高点

D．

y随x的增大而增大

将二次函数y=x²的图象向右平移一个单位长度，再向上平移3个单位长度所得的图象解析式为（ ）

A．y=（x-1）^2+3	B．y=（x+1）^2+3
C．y=（x-1）^2-3	D．y=（x+1）^2-3

某種新型禮炮的升空高度h（m）與飛行時間t（s）的關系式是h=─（5/2）t²+20t+1，若這種禮炮在點火升空到最高點處引爆，則從點火升空到引爆需要的時間為（  ）．

A．3S

B．4S

C．5S

D．6S

如图，二次函数y＝ax²＋bx＋c的图象的顶点在第一象限，且过点（0，1）和（－1，0）．下列结论：①ab＜0， ②b²＞4a， ③0＜b＜1， ④0＜a＋b＋c＜2， ⑤当x＞－1时，y＞0． 其中正确结论的个数是

A．2个

B．3个

C．4个

D．5个

抛物线y=﹣x²+bx+c的部分图象如图所示，要使y＞0，则x的取值范围是（ ）

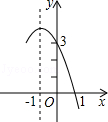
A．﹣4＜x＜1

B．﹣3＜x＜1

C．x＜﹣4或x＞1

D．x＜﹣3或x＞1

抛物线y=3x²向左平移1个单位，再向上平移2个单位，所得到的抛物线是（ ）

A．y=3（x﹣1）^2﹣2

B．y=3（x+1）^2﹣2

C．y=3（x+1）^2+2

D．y=3（x﹣1）^2+2

如图，抛物线y=ax²+bx+c（a＞0）的对称轴是直线x=1，且经过点P（3，0），则a﹣b+c的值为（   ）

A．0

B．﹣1

C．1

D．2

对于二次函数的图象，下列说法正确的是（ ）

A．开口向上

B．对称轴是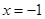

C．顶点坐标是（1，2）

D．与x轴有两个交点

把抛物线向左平移3个单位，再向上平移2个单位所得抛物线的解析式为（    ）

A．	B．
C．	D．

已知点（-1，y₁），（-2，y₂），（2，y₃）在函数y=2（x-1）²的图象上，则y₁、y₂、y₃的大小关系是（  ）

A．y1＞y2＞y3

B．y2＞y1＞y3

C．y2＞y3＞y1

D．y3＞y1＞y2

在二次函数y=ax²+bx+c，x与y的部分对应值如下表：

x	…	-2	0	2	3	…
y	…	8	0	0	3	…

则下列说法：
①图象经过原点；
②图象开口向下；
③图象经过点（-1，3）；
④当x＞0时，y随x的增大而增大；
⑤方程ax²+bx+c=0有两个不相等的实数根．
其中正确的是（）
A、①②③        B、①③⑤         C、①③④           D、①④⑤