如图在Rt△ABC中,∠ACB=90°,∠BAC=30°,AB=2,D是AB边上的一个动点(不与点A、B重合),过点D作CD的垂线交射线CA于点E.设AD=x,CE=y,则下列图象中,能表示y与x的函数关系图象大致是( )

A. B.
B. C.
C. D.
D.
王芳将如图所示的三条水平直线m1,m2,m3的其中一条记为x轴(向右为正方向),三条竖直直线m4,m5,m6的其中一条记为y轴(向上为正方向),并在此坐标平面内画出了抛物线y=ax2-6ax-3,则她所选择的x轴和y轴分别为( )

| A.m1,m4 | B.m2,m3 | C.m3,m6 | D.m4,m5 |
如图是一个横断面为抛物线形状的拱桥,当水面宽4m时,拱顶(拱桥洞的最高点)离水面2m,当水面下降1m时,水面的宽度为( )

| A.3 | B.2 |
C.3 |
D.2 |
抛物线y=x2+x+p(p≠0)与x轴相交,其中一个交点的横坐标是p.那么该抛物线的顶点的坐标是( )
| A.(0,-2) | B.( , , ) ) |
C.( , , ) ) |
D.( , , ) ) |
已知抛物线 的部分图象如图所示,若y<0,则x的取值范围是( )
的部分图象如图所示,若y<0,则x的取值范围是( )

| A.﹣1<x<3 | B.﹣1<x<4 |
| C.x<﹣1或 x>4 | D.x<﹣1或 x>3 |
如图,在平面直角坐标系中,抛物线y=ax2+bx+5经过A(2,5),B(﹣1,2)两点,若点C在该抛物线上,则C点的坐标可能是( )
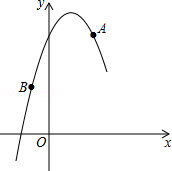
| A.(﹣2,0) | B.(0.5,6.5) | C.(3,2) | D.(2,2) |
如图,将抛物线l:y=ax2-2x+a2-4(a为常数)向左并向上平移,使顶点Q的对应点Q′,抛物线l与x轴的右交点P的对应点P′分别在两坐标轴上,则抛物线l与x轴的交点E的对应点的坐标为( )

A.(-1,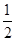 ) ) |
B.(0,0) | C.(-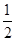 ,1) ,1) |
D.(-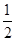 ,0) ,0) |
若抛物线y=x2-2x+c与y轴的交点为(0,-3),则下列说法不正确的是( )
| A.抛物线开口向上 |
| B.抛物线的对称轴是x=1 |
| C.当x=1时,y的最大值为-4 |
| D.抛物线与x轴的交点为(-1,0),(3,0) |
一个小球被抛出后,如果距离地面的高度h(米)和运行时间t(秒)的函数解析式为h=-5t2+10t+1,那么小球到达最高点时距离地面的高度是( )
| A.1米 | B.3米 | C.5米 | D.6米 |
如图是二次函数 (
( )图象的一部分,对称轴是直线x=﹣2.关于下列结论:①ab<0;②
)图象的一部分,对称轴是直线x=﹣2.关于下列结论:①ab<0;② ;③9a﹣3b+c<0;④b﹣4a=0;⑤方程
;③9a﹣3b+c<0;④b﹣4a=0;⑤方程 的两个根为
的两个根为 ,
, ,其中正确的结论有( )
,其中正确的结论有( )
| A.①③④ | B.②④⑤ | C.①②⑤ | D.②③⑤ |
图2是图1中拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可近似看成抛物线 ,桥拱与桥墩AC的交点C恰好在水面,有AC⊥x轴,若OA=10米,则桥面离水面的高度AC为( )
,桥拱与桥墩AC的交点C恰好在水面,有AC⊥x轴,若OA=10米,则桥面离水面的高度AC为( )
A. 米 米 |
B. 米 米 |
C. 米 米 |
D. 米 米 |
抛物线y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y= 在同一平面直角坐标系内的图象大致为( )
在同一平面直角坐标系内的图象大致为( )
如图,已知二次函数 (
( )的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
)的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
①当x>3时,y<0;
②3a+b<0;
③ ;
;
④ ;
;
其中正确的结论是( )
| A.①③④ | B.①②③ | C.①②④ | D.①②③④ |