如果二次函数 的图象如图所示,那么一次函数
的图象如图所示,那么一次函数 和反比例函数
和反比例函数 在同一坐标系中的图象大致是( )
在同一坐标系中的图象大致是( )
A. |
B. |
C. |
D. |
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则函数y= 与y=bx+c在同一直角坐标系内的大致图象是( )
与y=bx+c在同一直角坐标系内的大致图象是( )
A. |
B. |
C. |
D. |
如图,抛物线 交
交 轴于点A(
轴于点A( ,0)和B(
,0)和B( , 0),交
, 0),交 轴于点C,抛物线的顶点为D。下列四个命题:
轴于点C,抛物线的顶点为D。下列四个命题:
①当 时,
时, ;
;
②若 ,则
,则 ;
;
③抛物线上有两点P( ,
, )和Q(
)和Q( ,
, ),若
),若 ,且
,且 ,则
,则 ;
;
④点C关于抛物线对称轴的对称点为E,点G,F分别在 轴和
轴和 轴上,当
轴上,当 时,四边形EDFG周长的最小值为
时,四边形EDFG周长的最小值为 。
。
其中真命题的序号是( )
A.① B.② C.③ D.④
如图,抛物线y=﹣2x2+8x﹣6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )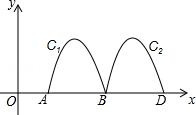
A.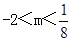 B.
B.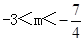
C.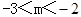 D.
D.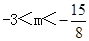
将抛物线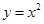 向右平移2个单位,再向上平移3个单位后,抛物线的解析式为( )
向右平移2个单位,再向上平移3个单位后,抛物线的解析式为( )
A. |
B. |
C.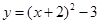 |
D.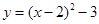 |
一次函数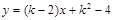 的图象经过原点,则
的图象经过原点,则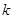 的值为( ).
的值为( ).
| A.2 | B.-2 | C.2或-2 | D.3 |
在平面直角坐标系中,抛物线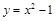 与
与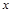 轴的交点的个数是( )
轴的交点的个数是( )
| A.3 | B.2 | C.1 | D.0 |
将抛物线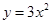 先沿
先沿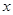 轴向右平移1个单位, 再沿
轴向右平移1个单位, 再沿 轴向上移2个单位,所得抛物线的解析式是( )
轴向上移2个单位,所得抛物线的解析式是( )
A.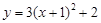 |
B.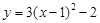 |
C.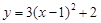 |
D.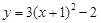 |
如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=3时,这两个二次函数的最大值之和等于( )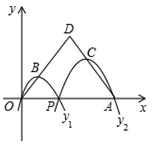
A.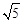 B.
B. C.3 D.4
C.3 D.4
如图,把抛物线y=x2与直线y=1围成的图形OABC绕原点O顺时针旋转90°后,再沿x轴向右平移1个单位得到图形O1A1B1C1,则下列结论错误的是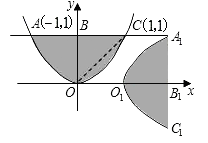
| A.点O1的坐标是(1,0) |
| B.点C1的坐标是(2,-1) |
| C.四边形OBA1B1是矩形 |
| D.若连接OC,则梯形OCA1B1的面积是3 |
二次函数y=a 的图象如图所示,
的图象如图所示,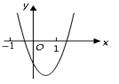
则一次函数y=bx+ 与反比例函数y=
与反比例函数y= 在同一坐标系内的图象大致为( )
在同一坐标系内的图象大致为( )



如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和B(B,0),交y轴于点C,抛物线的顶点为D.下列四个判断:①当x>0时,y>0;②若a=-1,则b=4;③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1< x2,且x1+ x2>2,则y1> y2;④点C关于抛物线对称轴的对称点为E,点G,F分别在x轴和y轴上,当m=2时,四边形EDFG周长的最小值为 ,其中正确判断的序号是( )
,其中正确判断的序号是( )
(A)① (B)②
(C)③ (D)④