河北省邯郸市魏县中考二模数学试卷
如图,△ABC中,E, D分别上边AB,AC的中点,若DE=3,则BC=( )
A.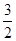 |
B.9 | C.6 | D.5 |
如图,在△ABC中,D是BC上延长线上一点,∠B=40°,∠ACD=120°,则∠A等于( )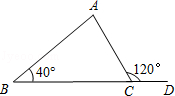
| A.20° | B.30° | C.70° | D.80° |
若直线y=mx+2m-3经过二、三、四象限,则m的取值范围是( )
A.m<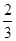 |
B.m>0 | C.m>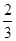 |
D.m<0 |
如图,将长为2,宽为1的矩形纸片分割成n个三角形后,拼成面积为2的正方形,则n可能是( )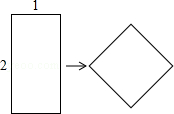
| A.2或4 | B.2或3 | C.3或5 | D.2或5 |
一个小球被抛出后,如果距离地面的高度h(米)和运行时间t(秒)的函数解析式为h=-5t2+10t+1,那么小球到达最高点时距离地面的高度是( )
| A.1米 | B.3米 | C.5米 | D.6米 |
如图是由6个相同的小正方体搭成的立体图形,若由图①变到图②,则( )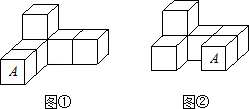
| A.主视图改变,俯视图改变 |
| B.主视图不变,俯视图改变 |
| C.主视图不变,俯视图不变 |
| D.主视图改变,俯视图不变 |
甲、乙两名同学在一次用频率去估计概率的实验中统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的实验可能是( )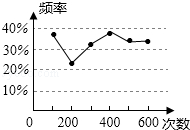
| A.从一装有2个白球和1个红球的袋子中任取一球,取到红球的概率 |
| B.掷一枚正六面体的骰子,出现1点的概率 |
| C.抛一枚硬币,出现正面的概率 |
| D.任意写一个整数,它能被2整除的概率 |
如图,点C在∠AOB的边OB上,用尺规作出了∠BCN=∠AOC,作图痕迹中,弧FG是( )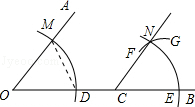
| A.以点C为圆心,OD为半径的弧 |
| B.以点C为圆心,DM为半径的弧 |
| C.以点E为圆心,OD为半径的弧 |
| D.以点E为圆心,DM为半径的弧 |
如图,为测量学校旗杆的高度,小东用长为3.2m的竹竿作测量工具,移动竹竿,使竹竿顶端与旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8m,与旗杆相距22m,则旗杆的高为( )m.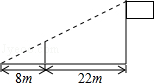
| A.8.8 | B.10 | C.12 | D.14 |
如图,点A的坐标为(-2,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为( )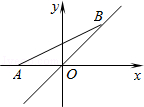
A.( , ,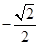 ) ) |
B.(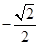 , ,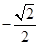 ) ) |
C.(0,0) | D.(-1,-1) |
某县10名学生参加汉字听写大赛,他们得分情况如下表:
| 人数 |
3 |
4 |
2 |
1 |
| 分数 |
80 |
85 |
90 |
95 |
那么这10名学生所得分数的中位数和众数分别是( )
A.85和82.5 B.85.5和85 C.85和85 D.85.5和80
已知代数式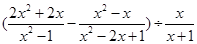 ,请解答下列问题:
,请解答下列问题:
(1)当x=2sin30°+tan60°时,求原代数式的值;
(2)当x在实数范围内取值时,原代数式的值能等于-1吗?说明理由.
已知:如图,在平面直角坐标系中,直线AB与反比例函数y=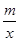 (m>0)的图象交与点A(1,4)、B(a、b),q其中a>1.过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,AC与BD相交于点M,连接CD.
(m>0)的图象交与点A(1,4)、B(a、b),q其中a>1.过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,AC与BD相交于点M,连接CD.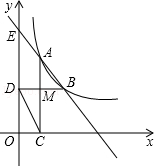
(1)求该反比例函数的解析式;
(2)求证:CD∥AB.
如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°.得到△ADE,连接BD,CE交于点F.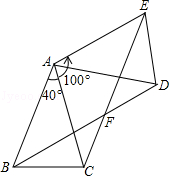
(1)求证:△ABD≌△ACE;
(2)求∠ACE的度数;
(3)求证:四边形ABFE是菱形.
如图,2×2网格(每个小正方形的边长为1)中有A,B,C,D,E,F,G、H,O九个格点.抛物线l的解析式为y=(-1)nx2+bx+c(n为整数).
(1)n为奇数,且l经过点H(0,1)和C(2,1),求b,c的值,并直接写出哪个格点是该抛物线的顶点;
(2)n为偶数,且l经过点A(1,0)和B(2,0),通过计算说明点F(0,2)和H(0,1)是否在该抛物线上;
(3)若l经过这九个格点中的三个,直接写出所有满足这样条件的抛物线条数.
图1和图2,半圆O的直径AB=2,点P(不与点A,B重合)为半圆上一点,将图形延BP折叠,分别得到点A,O的对称点A′,O′,设∠ABP=α.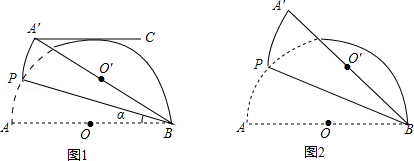
(1)当α=15°时,过点A′作A′C∥AB,如图1,判断A′C与半圆O的位置关系,并说明理由.
(2)如图2,当α= °时,BA′与半圆O相切.当α= °时,点O′落在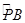 上.
上.
(3)当线段BO′与半圆O只有一个公共点B时,求α的取值范围.
如图,已知正方形ABCD中,边长为10厘米,点E在AB边上,BE=6厘米.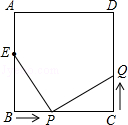
(1)如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPE与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPE与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿正方形ABCD四边运动,求经过多长时间点P与点Q第一次在正方形ABCD边上的何处相遇?
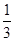
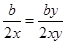
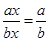
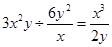

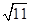 <b,则a+b的值是( )
<b,则a+b的值是( )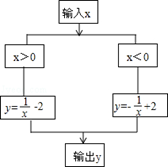
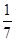
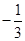

 的值为 .
的值为 .
 粤公网安备 44130202000953号
粤公网安备 44130202000953号