初中数学二次函数在给定区间上的最值试题

如图，在平面直角坐标系中，已知点A的坐标是（4，0），并且OA=OC=4OB，动点P在过A，B，C三点的抛物线上．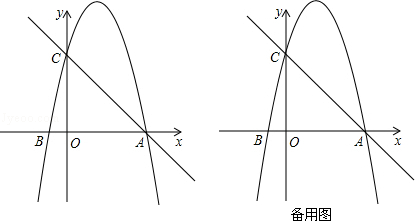

（1）求抛物线的解析式；
（2）是否存在点P，使得△ACP是以AC为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，说明理由；
（3）过动点P作PE垂直于y轴于点E，交直线AC于点D，过点D作x轴的垂线．垂足为F，连接EF，当线段EF的长度最短时，求出点P的坐标．

如图，在平面直角坐标系中，抛物线（）与x轴交于A、B两点（点A在点B的右侧），与y轴交于点C，点A的坐标为（4，0），抛物线的对称轴是直线．

（1）求抛物线的解析式；
（2）M为第一象限内的抛物线上的一个点，过点M作MG⊥x轴于点G，交AC于点H，当线段CM=CH时，求点M的坐标；
（3）在（2）的条件下，将线段MG绕点G顺时针旋转一个角α（0°＜α＜90°），在旋转过程中，设线段MG与抛物线交于点N，在线段GA上是否存在点P，使得以P、N、G为顶点的三角形与△ABC相似？如果存在，请求出点P的坐标；如果不存在，请说明理由．

为了迎接无锡市排球运动会，市排协准备新购一批排球．
（1）张会长问小李：“我们现在还有多少个排球？”，小李说：“两年前我们购进100个新排球，由于训练损坏，现在还有81个球．”，假设这两年平均每年的损坏率相同，求损坏率．
（2）张会长说：“我们协会现有训练队是奇数个，如果新购进的排球，每队分8个球，新球正好都分完；如果每队分9个球，那么有一个队分得的新球就不足6个，但超过2个．”请问市排协准备新购排球多少个？该协会有多少个训练队？
（3）张会长要求小李去买这批新排球，小李看到某体育用品商店提供如下信息：
信息一：可供选择的排球有A、B、C三种型号，但要求购买A、B型号数量相等．
信息二：如表：

型号	每个型号批发单价（元）	每年每个型号排球的损坏率
A	30	0．2
B	20	0．3
C	50	0．1

 
设购买A、C型号排球分别为a个、b个，请你能帮助小李制定一个购买方案．要求购买总费用w（元）最少，而且要使这批排球两年后没有损坏的个数不少于27个．

抛物线y=x²+mx+n可以由抛物线y=x²向上平移2个单位，再向左平移3个单位得到，则mn值为（    ）

A．6

B．12

C．54

D．66

如图，在平面直角坐标系中，已知OA=2，OC=4，⊙M与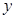轴相切于点C，与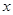轴交于A，B两点，∠ACD=90°，抛物线经过A，B，C三点．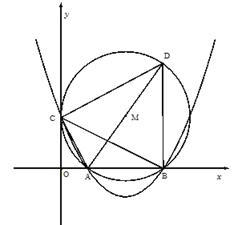

（1）求证：∠CAO=∠CAD；
（2）求弦BD的长；
（3）在抛物线的对称轴上是否存在点P使ΔPBC是以BC为腰的等腰三角形？若存在，求出点P的坐标；若不存在，请说明理由．

（本小题14分）如图，在平面直角坐标系中，矩形OCDE的三个顶点分别是C（3，0），D（3，4），E（0，4）．点A在DE上，以A为顶点的抛物线过点C，且对称轴x=1交x轴于点B．连接EC，AC．点P，Q为动点，设运动时间为t秒．

（1）填空：点A坐标为 ；抛物线的解析式为            ．
（2）在图1中，若点P在线段OC上从点O向点C以1个单位/秒的速度运动，同时，点Q在线段CE上从点C向点E以2个单位/秒的速度运动，当一个点到达终点时，另一个点随之停止运动．当t为何值时，△PCQ为直角三角形？
（3）在图2中，若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动，过点P做PF⊥AB，交AC于点F，过点F作FG⊥AD于点G，交抛物线于点Q，连接AQ，CQ．当t为何值时，△ACQ的面积最大？最大值是多少？

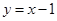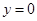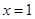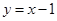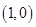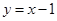我们将使得函数值为零的自变量的值称为函数的零点值，此时的点称为函数的零点．例如，对于函数，令，可得，我们就说1是函数的零点值，点是函数的零点．
已知二次函数．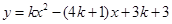
（1）若函数有两个不重合的零点时，求k的取值范围；
（2）若函数的两个零点都是整数点，求整数k的值；
（3）当k<0时，在（2）的条件下，函数的两个零点分别是点A，B（点A在点B的左侧），将二次函数的图象在点A，B间的部分（含点A和点B）向左平移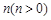个单位后得到的图象记为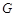，同时将直线向上平移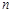个单位．请结合图象回答：当平移后的直线与图象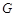有公共点时，求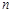的取值范围．

如图，二次函数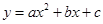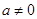（）的图象经过点（0，3），且当x=1时，y有最小值2．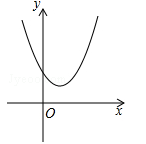

（1）求a，b，c的值；
（2）设二次函数（k为实数），它的图象的顶点为D．
①当k=1时，求二次函数的图象与x轴的交点坐标；
②请在二次函数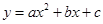与的图象上各找出一个点M，N，不论k取何值，这两个点始终关于x轴对称，直接写出点M，N的坐标（点M在点N的上方）；
③过点M的一次函数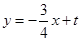的图象与二次函数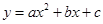的图象交于另一点P，当k为何值时，点D在∠NMP的平分线上？
④当k取﹣2，﹣1，0，1，2时，通过计算，得到对应的抛物线的顶点分别为（﹣1，﹣6，），（0，﹣5），（1，﹣2），（2，3），（3，10），请问：顶点的横、纵坐标是变量吗？纵坐标是如何随横坐标的变化而变化的？

沿海开发公司准备投资开发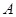、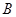两种新产品，通过市场调研发现：
（1）若单独投资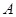种产品，则所获利润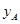（万元）与投资金额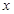（万元）之间满足正比例函数关系：；
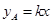（2）若单独投资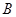种产品，则所获利润（万元）与投资金额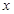（万元）之间满足二次函数关系：．
（3）根据公司信息部的报告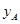，，（万元）与投资金额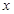（万元）的部分对应值如下表所示：

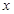	1	5
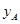	0.8	4
	3.8	15

（1）填空：     ；     ；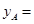
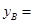（2）若公司准备投资20万元同时开发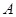、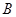两种新产品，设公司所获得的总利润为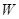（万元），试写出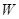与某种产品的投资金额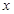（万元）之间的函数关系式；
（3）请你设计一个在（2）中能获得最大利润的投资方案，并求出按此方案能获得的最大利润是多少万元？

如图，在平面直角坐标系xoy中，点O为坐标原点，抛物线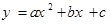与x轴交于点A（，0）、B（2，0），与y轴交于点C，以O为圆心，半径为1的⊙O恰好经过点C，与x轴的正半轴交于点D．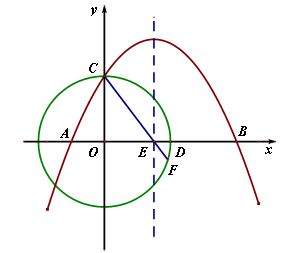

（1）求抛物线相应的函数表达式；
（2）抛物线的对称轴交x轴于点E，连结CE，并延长CE交⊙O于F，求EF的长．
（3）设点P（m，n）为⊙O上的任意一点，当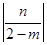的值最大时，求此时直线BP
相应的函数表达式．

抛物线y=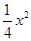+x+m的顶点在直线y=x+3上，过点F（-2，2）的直线交该抛物线于点M、N两点（点M在点N的左边），MA⊥x轴于点A，NB⊥x轴于点B．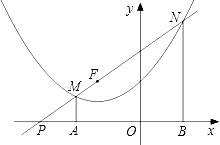

（1）先通过配方求抛物线的顶点坐标（坐标可用含m的代数式表示），再求m的值；
（2）设点N的横坐标为a，试用含a的代数式表示点N的纵坐标，并说明NF=NB；
（3）若射线NM交x轴于点P，且PA•PB=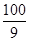，求点M的坐标．

如图，抛物线y=-x²-2x+3 的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，点D为抛物线的顶点．

（1）求A、B、C的坐标；
（2）点M为线段AB上一点（点M不与点A、B重合），过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N．若点P在点Q左边，当矩形PMNQ的周长最大时，求△AEM的面积；
（3）在（2）的条件下，当矩形PMNQ的周长最大时，连接DQ．过抛物线上一点F作y轴的平行线，与直线AC交于点G（点G在点F的上方）．若FG=2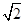DQ，求点F的坐标．

如图，已知抛物线y=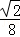（x+2）（x﹣4）与x轴交于点A、B（点A位于点B的左侧），与y轴交于点C，CD∥x轴交抛物线于点D，M为抛物线的顶点．
（1）求点A、B、C的坐标；
（2）设动点N（﹣2，n），求使MN+BN的值最小时n的值；
（3）P是抛物线上一点，请你探究：是否存在点P，使以P、A、B为顶点的三角形与△ABD相似（△PAB与△ABD不重合）？若存在，求出点P的坐标；若不存在，说明理由．

（本小题满分9分）如图，抛物线y=﹣x²+bx+c与x轴交于点A（1，0），B（-5，0）两点，直线y=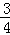x+3与y轴交于点C，与x轴交于点D．点P是x轴上方的抛物线上一动点，过点P作PF⊥x轴于点F，交直线CD于点E．设点P的横坐标为m．

（1）求抛物线的解析式；
（2）若PE=5EF，求m的值；
（3）若点E′是点E关于直线PC的对称点，是否存在点P，使点E′落在y轴上？若存在，请直接写出相应的点P的坐标；若不存在，请说明理由．

如图，已知抛物线 （）的顶点坐标为（4，），且与y轴交于点C（0，2），与x轴交于A、B两点（点A在点B的左边）.

（1）求抛物线的解析式及A、B两点的坐标；
（2）在（1）中抛物线的对称轴l上是否存在一点P，使AP+CP的值最小，若存在，求AP+CP的最小值；若不存在，请说明理由；
（3）在以AB为直径的⊙M中，CE与⊙M相切于点E，CE交x轴于点D，求直线CE的解析式．