初中数学二次函数在给定区间上的最值试题

如图（1），在平面直角坐标系xOy中，抛物线与x轴交于，与y轴交于C(0，3)，顶点为D(1,4)，对称轴为DE.
（1）抛物线的解析式是       ；
（2）如图（2），点P是AD上的一个动点，是P关于DE的对称点，连结PE，过作F∥PE交x轴于F. 设，求y关于x的函数关系式，并求y的最大值；
（3）在（1）中的抛物线上是否存在点Q，使△BCQ成为以BC为直角边的直角三角形？若存在，求出Q的坐标；若不存在，请说明理由.

如图，在平面直角坐标系中，抛物线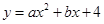经过A（－3，0）、B（4，0）两点，且与y轴交于点C，D（，0）．动点P从点A出发，沿线段AB以每秒1个单位长度的速度向点B移动，同时动点Q从点C出发，沿线段CA以某一速度向点A移动．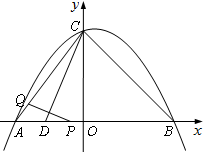

（1）求该抛物线的解析式；
（2）若经过t秒的移动，线段PQ被CD垂直平分，求此时t的值；
（3）在第一象限的抛物线上取一点G，使得S_△GCB=S_△GCA，再在抛物线上找点E（不与点A、B、C重合），使得∠GBE=45°，求E点的坐标．

如图，在Rt△ABC中，∠ACB=90°，AC=8cm，AB=10cm．点P从点A出发，以5cm/s的速度从点A运动到终点B；同时，点Q从点C出发，以3cm/s的速度从点C运动到终点B，连结PQ；过点P作PD⊥AC交AC于点D，将△APD沿PD翻折得到△A′PD，以A′P和PB为邻边作▱A′PBE，A′E交射线BC于点F，交射线PQ于点G．设▱A′PBE与四边形PDCQ重叠部分图形的面积为Scm²，点P的运动时间为ts．
（1）当t为何值时，点A′与点C重合；
（2）用含t的代数式表示QF的长；
（3）求S与t的函数关系式；
（4）请直接写出当射线PQ将▱A′PBE分成的两部分图形的面积之比是1：3时t的值．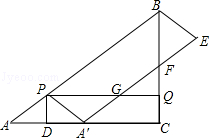

已知，抛物线y=ax²+bx+4（a≠0）与x轴交于A（﹣2，0）、B（8，0）两点，与y轴交于点C．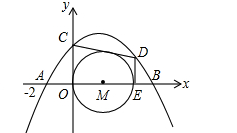

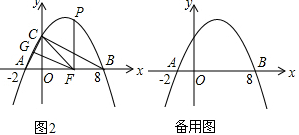
（1）求此抛物线的解析式；
（2）如图1，点E是线段OB上一动点，过点E作DE⊥x轴，交抛物线于点D，若直线CD与以OE为直径的⊙M相切，试求出点E的坐标；
（3）如图2，在抛物线上是否存在一点P，过点P作x轴的垂线，垂足为F，过点F作FG∥BC，交线段AC于点G，连接FC，使△BCF∽△CFG？若存在，求出点P的坐标；若不存在，请说明理由．

如图，在平面直角坐标系中，己知点O（0，0），A（5，0），B（4，4）．
（1）求过O、B、A三点的抛物线的解析式．
（2）在第一象限的抛物线上存在点M，使以O、A、B、M为顶点的四边形面积最大，求点M的坐标．
（3）作直线x=m交抛物线于点P，交线段OB于点Q，当△PQB为等腰三角形时，求m的值．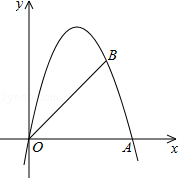

如图，在平面直角坐标系中，已知点A的坐标是（4，0），并且OA=OC=4OB，动点P在过A，B，C三点的抛物线上．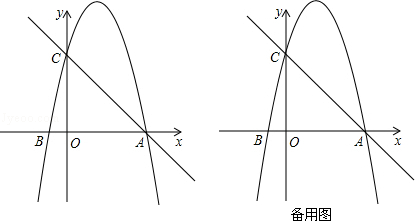

（1）求抛物线的解析式；
（2）是否存在点P，使得△ACP是以AC为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，说明理由；
（3）过动点P作PE垂直于y轴于点E，交直线AC于点D，过点D作x轴的垂线．垂足为F，连接EF，当线段EF的长度最短时，求出点P的坐标．

如图1，在平面直角坐标系xOy中，点M为抛物线的顶点，过点（0，4）作x轴的平行线，交抛物线于点P、Q（点P在Q的左侧），PQ=4．
（1）求抛物线的函数关系式，并写出点P的坐标；
（2）小丽发现：将抛物线绕着点P旋转180°，所得新抛物线的顶点恰为坐标原点O，你认为正确吗？请说明理由；
（3）如图2，已知点A（1，0），以PA为边作矩形PABC（点P、A、B、C按顺时针的方向排列），．
①写出C点的坐标：C（       ，       ）（坐标用含有t的代数式表示）；
②若点C在题（2）中旋转后的新抛物线上，求t的值．

如图，在平面直角坐标系中，抛物线（）与x轴交于A、B两点（点A在点B的右侧），与y轴交于点C，点A的坐标为（4，0），抛物线的对称轴是直线．

（1）求抛物线的解析式；
（2）M为第一象限内的抛物线上的一个点，过点M作MG⊥x轴于点G，交AC于点H，当线段CM=CH时，求点M的坐标；
（3）在（2）的条件下，将线段MG绕点G顺时针旋转一个角α（0°＜α＜90°），在旋转过程中，设线段MG与抛物线交于点N，在线段GA上是否存在点P，使得以P、N、G为顶点的三角形与△ABC相似？如果存在，请求出点P的坐标；如果不存在，请说明理由．

如图，二次函数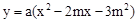（其中a，m是常数，且a>0，m>0）的图象与x轴分别交于点A，B（点A位于点B的左侧），与y轴交于点C(0，－3)，点D在二次函数的图象上，CD∥AB，连接AD．过点A作射线AE交二次函数的图象于点E，AB平分∠DAE．
（1）用含m的代数式表示a；
（2）)求证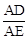：为定值；
（3）设该二次函数图象的顶点为F．探索：在x轴的负半轴上是否存在点G，连接CF，以线段GF、AD、AE的长度为三边长的三角形是直角三角形？如果存在，只要找出一个满足要求的点G即可，并用含m的代数式表示该点的横坐标；如果不存在，请说明理由．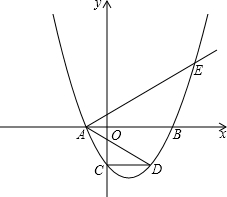

为了迎接无锡市排球运动会，市排协准备新购一批排球．
（1）张会长问小李：“我们现在还有多少个排球？”，小李说：“两年前我们购进100个新排球，由于训练损坏，现在还有81个球．”，假设这两年平均每年的损坏率相同，求损坏率．
（2）张会长说：“我们协会现有训练队是奇数个，如果新购进的排球，每队分8个球，新球正好都分完；如果每队分9个球，那么有一个队分得的新球就不足6个，但超过2个．”请问市排协准备新购排球多少个？该协会有多少个训练队？
（3）张会长要求小李去买这批新排球，小李看到某体育用品商店提供如下信息：
信息一：可供选择的排球有A、B、C三种型号，但要求购买A、B型号数量相等．
信息二：如表：

型号	每个型号批发单价（元）	每年每个型号排球的损坏率
A	30	0．2
B	20	0．3
C	50	0．1

 
设购买A、C型号排球分别为a个、b个，请你能帮助小李制定一个购买方案．要求购买总费用w（元）最少，而且要使这批排球两年后没有损坏的个数不少于27个．

抛物线y=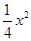+x+m的顶点在直线y=x+3上，过点F（-2，2）的直线交该抛物线于点M、N两点（点M在点N的左边），MA⊥x轴于点A，NB⊥x轴于点B．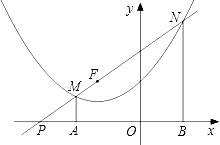

（1）先通过配方求抛物线的顶点坐标（坐标可用含m的代数式表示），再求m的值；
（2）设点N的横坐标为a，试用含a的代数式表示点N的纵坐标，并说明NF=NB；
（3）若射线NM交x轴于点P，且PA•PB=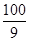，求点M的坐标．

如图，抛物线y=-x²-2x+3 的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，点D为抛物线的顶点．

（1）求A、B、C的坐标；
（2）点M为线段AB上一点（点M不与点A、B重合），过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N．若点P在点Q左边，当矩形PMNQ的周长最大时，求△AEM的面积；
（3）在（2）的条件下，当矩形PMNQ的周长最大时，连接DQ．过抛物线上一点F作y轴的平行线，与直线AC交于点G（点G在点F的上方）．若FG=2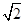DQ，求点F的坐标．

如图，已知抛物线y=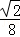（x+2）（x﹣4）与x轴交于点A、B（点A位于点B的左侧），与y轴交于点C，CD∥x轴交抛物线于点D，M为抛物线的顶点．
（1）求点A、B、C的坐标；
（2）设动点N（﹣2，n），求使MN+BN的值最小时n的值；
（3）P是抛物线上一点，请你探究：是否存在点P，使以P、A、B为顶点的三角形与△ABD相似（△PAB与△ABD不重合）？若存在，求出点P的坐标；若不存在，说明理由．

（本小题满分9分）如图，抛物线y=﹣x²+bx+c与x轴交于点A（1，0），B（-5，0）两点，直线y=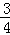x+3与y轴交于点C，与x轴交于点D．点P是x轴上方的抛物线上一动点，过点P作PF⊥x轴于点F，交直线CD于点E．设点P的横坐标为m．

（1）求抛物线的解析式；
（2）若PE=5EF，求m的值；
（3）若点E′是点E关于直线PC的对称点，是否存在点P，使点E′落在y轴上？若存在，请直接写出相应的点P的坐标；若不存在，请说明理由．

如图，在平面直角坐标系xOy中，直线y=x+4与坐标轴分别交于A、B两点，过A、B两点的抛物线为y=－x²+bx+c．点D为线段AB上一动点，过点D作CD⊥x轴于点C，交抛物线于点E．

（1）求抛物线的解析式．
（2）当DE=4时，求四边形CAEB的面积．
（3）连接BE，是否存在点D，使得△DBE和△DAC相似？若存在，直接写出点D坐标；若不存在，说明理由．