如图,抛物线y=ax2+bx+c的对称轴是x=,小亮通过观察得出了下面四条信息:①c<0,②abc<0,③a-b+c>0,④2a-3b=0。你认为其中正确的有____________________。(填序号)
(本题12分) 如图,在平面直角坐标系中,二次函数 的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.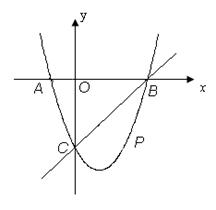
(1)求b,c的值.
(2)连结PO、PC,并把△POC沿CO翻折,得到四边形 ,那么是否存在点P,使四边形
,那么是否存在点P,使四边形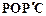 为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形 ABPC的面积最大,并求出此时P点的坐标和四边形ABPC的最大面积.
(本题8分) 已知二次函数 的图象与
的图象与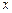 轴两交点的坐标分别为(
轴两交点的坐标分别为(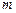 ,0),(
,0),(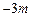 ,0)(
,0)( ).
).
(1)证明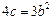 ;
;
(2)若该函数图象的对称轴为直线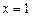 ,试求二次函数的最小值.
,试求二次函数的最小值.
(本题8分)
已知:抛物线 与x轴相交于A、B两点(A点在B点的左侧),顶点为P.
与x轴相交于A、B两点(A点在B点的左侧),顶点为P.
(1)求A、B、P三点坐标;
(2)画出此抛物线的简图,并根据简图直接写出当 时,函数值y的取值范围
时,函数值y的取值范围
如图,是二次函数y=ax2+bx+c图象的一部分,其对称轴为直线x=1,
若其与x轴一交点为A(3,0),则由图象可知,不等式 的解集是
的解集是
如图,直线y=hx+d与x轴和y轴分别相交于点A(-1,0),B(0,1),与双曲线y= 在第一象限相交于点C;以AC为斜边、
在第一象限相交于点C;以AC为斜边、 为内角的直角三角形,与以CO为对角线、一边在x轴上的矩形面积相等;点C,P在以B为顶点的抛物线y=
为内角的直角三角形,与以CO为对角线、一边在x轴上的矩形面积相等;点C,P在以B为顶点的抛物线y= 上;直线y=hx+d、双曲线y=
上;直线y=hx+d、双曲线y= 和抛物线
和抛物线 同时经过两个不同的点C,D
同时经过两个不同的点C,D

(1)确定t的值
(2)确定m , n , k的值
(3)若无论a , b , c何值,抛物线 都不经点P,请确定P坐标
都不经点P,请确定P坐标
抛物线 的顶点坐标是( )
的顶点坐标是( )
| A.(0,-1) | B.(-1,1) | C.(-1,0) | D.(1,0) |
如图,在平面直角坐标系 中,抛物线
中,抛物线 向左平移1个单位,再向下平移4个单位,得到抛物线
向左平移1个单位,再向下平移4个单位,得到抛物线 .所得抛物线与
.所得抛物线与 轴交于
轴交于 两点(点
两点(点 在点
在点 的左边),与
的左边),与 轴交于点
轴交于点 ,顶点为
,顶点为 .
.
(1)求 的值;
的值;
(2)判断 的形状,并说明理由;
的形状,并说明理由;
(3)在线段 上是否存在点
上是否存在点 ,使
,使 与
与 相似.若存在,求出点
相似.若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(12分)
如图,在平面直角坐标系中,二次函数 的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的表达式.
(2)连结PO、PC,并把△POC沿CO翻折,得到四边形POP C, 那么是否存在点P,使四边形POP
C, 那么是否存在点P,使四边形POP C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形 ABPC的面积最大并求出此时P点的坐标和四边形ABPC的最大面积.
(10分) 恩施州绿色、富硒产品和特色农产品在国际市场上颇具竞争力,其中香菇远销日本和韩国等地.上市时,外商李经理按市场价格10元/千克在我州收购了2000千克香菇存放入冷库中.据预测,香菇的市场价格每天每千克将上涨0.5元,但冷库存放这批香菇时每天需要支出各种费用合计340元,而且香菇在冷库中最多保存110天,同时,平均每天有6千克的香菇损坏不能出售.
(1)若存放 天后,将这批香菇一次性出售,设这批香菇的销售总金额为
天后,将这批香菇一次性出售,设这批香菇的销售总金额为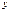 元,试写出
元,试写出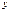 与
与 之间的函数关系式.
之间的函数关系式.
(2)李经理想获得利润22500元,需将这批香菇存放多少天后出售?(利润=销售总金额-收购成本-各种费用)
(3)李经理将这批香菇存放多少天后出售可获得最大利润?最大利润是多少?
已知抛物线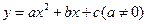 顶点为C(1,1)且过原点O.过抛物线上一点P(x,y)向直线
顶点为C(1,1)且过原点O.过抛物线上一点P(x,y)向直线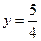 作垂线,垂足为M,连FM(如图).
作垂线,垂足为M,连FM(如图).
(1)求字母a,b,c的值;
(2)在直线x=1上有一点 ,求以PM为底边的等腰三角形PFM的P点的坐标,并证明此时△PFM为正三角形;
,求以PM为底边的等腰三角形PFM的P点的坐标,并证明此时△PFM为正三角形;
(3)对抛物线上任意一点P,是否总存在一点N(1,t),使PM=PN恒成立,若存在请求出t值,若不存在请说明理由.
将抛物线 绕它的顶点旋转180°,所得抛物线的解析式是()
绕它的顶点旋转180°,所得抛物线的解析式是()
A. |
B. |
C. |
D. |