初中数学二次函数在给定区间上的最值试题

函数的图像是开口向下的抛物线，则       。

如图所示，抛物线y=-x²+mx+n经过点A（1,0）和点C(4,0)，与y轴交于点B。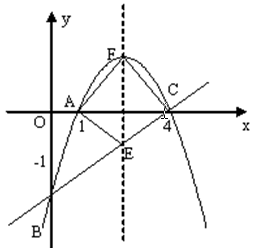

（1）求抛物线所对应的解析式。
（2）连接直线BC,抛物线的对称轴与BC交于点E，F为抛物线的顶点，求四边形AECF的面积。

在平面直角坐标系 中，抛物线的开口向下，且抛物线与轴的交于点，与 轴交于，两点，（在左侧）. 点的纵坐标是.

（1）求抛物线的解析式；
（2）求直线的解析式；
（3）将抛物线在点左侧的图形（含点）记为.若直线与直线平行，且与
图形恰有一个公共点，结合函数图象写出的取值范围.

国家推行“节能减排\低碳经济”政策后，低排量的汽车比较畅销，某汽车经销商购进A，B两种型号的低排量汽车，其中A型汽车的进货单价比B型汽车的进货单价多2万元,花50万元购进A型汽车的数量与花40万元购进B型汽车的数量相等，销售中发现A型汽车的每周销量（台）与售价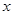（万元/台）满足函数关系式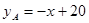，B型汽车的每周销量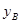（台）与售价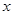万元/台）满足函数关系式．
（1）求A、B两种型号的汽车的进货单价；
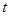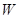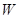（2）已知A型汽车的售价比B型汽车的人售价高2万元/台，设B型汽车售价为万元/台．每周销售这两种车的总利润为万元，求与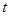的函数关系式，A、B两种型号的汽车售价各为多少时，每周销售这两种车的总利润最大？最大总利润是多少万元？

已知二次函数．
（1）在给出的直角坐标系中画出它的示意图；

（2）观察图象填空：
①当        时，随的增大而增大；
②使的的取值范围是       ；
③将图象向左平移1个单位再向上平移2个单位，所得的抛物线的解析式             ．

已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下结论：①a+b+c＜0；②a-b+c＜0；③b+2a＜0；④abc＞0．其中所有正确结论的序号是              （把你认为正确的结论序号都填上）．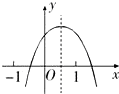

已知二次函数y=x²-2mx+m²-1．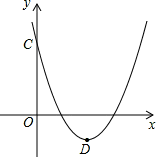

（1）当二次函数的图象经过坐标原点O（0，0）时，求二次函数的解析式；
（2）如图，当m=2时，该抛物线与y轴交于点C，顶点为D，求C、D两点的坐标；
（3）在（2）的条件下，x轴上是否存在一点P，使得PC+PD最短？若P点存在，求出P点的坐标；若P点不存在，请说明理由．

将二次函数y=x²的图象向右平移一个单位长度，再向上平移3个单位长度所得的图象解析式为（ ）

A．y=（x﹣1）^2+3

B．y=（x+1）^2+3

C．y=（x﹣1）^2﹣3

D．y=（x+1）^2﹣3

抛物线的顶点坐标是（  ）

A．（3，1）

B．（3，-1）

C．（-3，1）

D．（-3，-1）

（本题8分）为了改善小区环境，某小区决定要在一块一边靠墙（墙长25m）的空地上修建一个矩形绿化带ABCD，绿化带一边靠墙，另三边用总长为40m的栅栏围住（如图）．若设绿化带的BC边长为x m，绿化带的面积为y m²．

（1）求y与x之间的函数关系式，并写出自变量x的取值范围；
（2）当x为何值时，满足条件的绿化带的面积最大．

对于每个非零自然数n，抛物线y=x²-x+与x轴交于A_n、B_n两点，以表示这两点间的距离，则的值是          

抛物线y=－x²的顶点坐标为________；若点A（3，m）是此抛物线上一点，则m= ____；把此抛物线向下平移4个单位得到的抛物线的函数关系式是                   ．

如图，在平面直角坐标系中，已知点A（0，1）、B（3，5），以AB为边作如图所示的正方形ABCD，顶点在坐标原点的抛物线恰好经过点D，P为抛物线上的一动点．

（1）直接写出点D的坐标；
（2）求抛物线的解析式；
（3）求点P到点A的距离与点P到x轴的距离之差；
（4）当点P位于何处时，△APB的周长有最小值，并求出△APB的周长的最小值．

已知二次函数．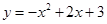

（1）求函数图像的顶点坐标，并画出这个函数的图像；
（2）根据图像，直接写出：
①当函数值y为正数时，自变量x的取值范围；
②当―2＜x＜2时，函数值y的取值范围．

请写出一个开口向上，与y轴交点的纵坐标为2的抛物线的函数表达式   ．