初中数学二次函数在给定区间上的最值试题

试写出一个开口方向向上，对称轴为直线x=2，且与y轴的交点坐标为（0，3）的抛物线的解析式为___________________

如图，小姚身高m在某次投篮中，球的运动路线是抛物线的一部分，若命中篮圈中心，则他与篮底的距离 是（   ）

A．3.5m

B．4m

C．4.5m

D．4.6m

把抛物线的图象向左平移1个单位，再向上平移6个单位，所得的抛物线的函数关系式是（   ）

A．

B．

C．

D．

已知二次函数=a（x－2）²＋k的图象开口向上，若点M（－2，y₁），N（－1，y₂），K（8，y₃）都在二次函数y=a（x－2）²＋k的图像上，则下列结论正确的是（  ）

A．y1＜y2＜y3

B．y2＜y1＜y3

C．y3＜y1＜y2

D．y1＜y3＜y2

如图，教练对小明推铅球的录像进行技术分析，发现铅球行进高度与水平距离之间的关系为，由此可知铅球推出的距离是        ．

已知二次函数，若，，那么它的图象大致是（    ）．

把抛物线向左平移个单位，然后向上平移个单位，则平移后抛物线的解析式为（    ）．

A．	B．
C．	D．

如图，直线y=﹣x+3与x轴，y轴分别交于B，C两点，抛物线y=﹣x²+bx+c经过B，C两点，点A是抛物线与x轴的另一个交点．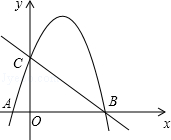

（1）求B、C两点坐标；
（2）求此抛物线的函数解析式；
（3）在抛物线上是否存在点P，使S_△PAB=S_△CAB，若存在，求出P点坐标，若不存在，请说明理由．

二次函数y=ax²+bx+c（a≠0）的图象如图所示，给出下列结论：

①b²﹣4ac＞0；
②2a+b＜0； 
③4a﹣2b+c=0；
④a：b：c=﹣1：2：3．
其中正确的个数是（ ）

A．1

B．2

C．3

D．4

已知抛物线与x轴相交于A（-1，0）,B（3，0）两点，顶点坐标为C（1，4）,
（1）求该抛物线解析式，
（2）判断开口方向以及增减情况

抛物线y=x²-（b-2）x+3b 的顶点在y轴上，则b的值为           。

二次函数y=ax²＋bx＋c（a≠0）的图象如图，下列结论正确的是（ ）

A．a<0

B．b^2－4ac<0

C．当－1<x<3时，y>0

D．－="1"

将抛物线y=3x²向左平移2个单位，再向下平移1个单位，所得抛物线为（ ）

A．y=3（x－2）^2－1	B．y=3（x－2）^2＋1
C．y=3（x＋2）^2－1	D．y=3（x＋2）^2＋1

在同一直角坐标系中，二次函数与一次函数y=2x的图象大致是（   ）.

二次函数的最小值是（   ）.]

A．－35

B．－30

C．－5

D．20