初中数学一元二次方程的最值试题

某商场销售一批名牌衬衫，平均每天可售出20件，每件赢利40元，为了扩大销售，增加赢利，尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件。求：
（1）若商场平均每天要赢利1200元，每件衬衫应降价多少元？
（2）每件衬衫降价多少元时，商场平均每天赢利最多？

某水果批发商场经销一种高档水果，如果每千克盈利10元，每天可售出500千克．经市场调查发现，在进货价不变的情况下，若每千克涨价1元，日销售量将减少20千克．现该商场要保证每天盈利6000元，同时又要使顾客得到实惠，那么每千克应涨价多少元？

某水果批发商场经销一种高档水果，如果每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，若每千克涨价1元，日销量减少20千克，现该商场要保证每天盈利6000元，同时又要使顾客得到实惠，那么每千克应涨价多少元？

某公司投资新建了一商场，共有商铺30间.据预测，当每间的年租金定为10万元时，可全部租出．每间的年租金每增加5000元，少租出商铺1间．该公司要为租出的商铺每间每年交各种费用1万元，未租出的商铺每间每年交各种费用5000元．
（1）当每间商铺的年租金定为15万元时，能租出多少间？
（2）当每间商铺的年租金定为多少万元时，该公司的年收益（收益＝租金－各种费用）为284万元？

对于任意实数a、b，定义f（a，b）=a²+5a-b，如：f（2，3）=2²+5×2-3，若f（x，2）=4，则实数x的值是（   ）

A．1或-6

B．-1或6

C．-5或1

D．5或-1

如图，四边形ABCD中，AD∥BC，∠A=90°，AD=1厘米，AB=3厘米，BC=5厘米，动点P从点B出发以1厘米/秒的速度沿BC方向运动，动点Q从点C出发以2厘米/秒的速度沿CD方向运动，P，Q两点同时出发，当点Q到达点D时停止运动，点P也随之停止，设运动时间为t秒（t＞0）．

（1）求线段CD的长；
（2）t为何值时，线段PQ将四边形ABCD的面积分为1：2两部分？
（3）伴随P，Q两点的运动，线段PQ的垂直平分线为l．
①t为何值时，l经过点C？
②求当l经过点D时t的值，并求出此时刻线段PQ的长．

某商品的进价为每件40元，售价为每件50元，每个月可卖出210件．如果每件商品的售价每上涨1元，则每个月少卖10件．当每件商品的售价定为多少元时，每个月的利润恰为2200元？

关于x的方程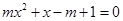，有以下三个结论：①当m=0时，方程只有一个实数解②当时，方程有两个不等的实数解③无论m取何值，方程都有一个负数解，其中正确的是          （填序号）

20．解方程：
（1）解方程：x²-6x-2=0；
（2）．

已知关于x的一元二次方程．
（1）若此方程有两个不相等的实数根，求实数k的取值范围；
（2）已知x=3是此方程的一个根，求方程的另一个根及k的值；
（3）当Rt△ABC的斜边长C=，且两条直角边A和B恰好是这个方程的两个根时，求Rt△ABC的面积．

2013年，东营市某楼盘以每平方米6500元的均价对外销售．因为楼盘滞销，房地产开发商为了加快资金周转，决定进行降价促销，经过连续两年下调后，2015年的均价为每平方米5265元．
（1）求平均每年下调的百分率；
（2）假设2016年的均价仍然下调相同的百分率，张强准备购买一套100平方米的住房，他持有现金20万元，可以在银行贷款30万元，张强的愿望能否实现？（房价每平方米按照均价计算）

已知关于x的一元二次方程（a+c）x²+2bx+（a－c）=0，其中a、b、c分别为△ABC三边的长．
（1）如果x=－1是方程的根，试判断△ABC的形状，并说明理由；
（2）如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由；
（3）如果△ABC是等边三角形，试求这个一元二次方程的根．

已知关于x的一元二次方程。
（1）求证：方程有两个不相等的实数根；
（2）若△ABC的两边AB、AC的长是方程的两个实数根，第三边BC的长为5。当△ABC是等腰三角形时，求k的值。

如图，在△ABC中，AB＝AC＝10cm，BD⊥AC于点D，且BD＝8cm．点M从点A出发，沿AC的方向匀速运动，速度为2cm/s；同时直线PQ由点B出发，沿BA的方向匀速运动，速度为1cm/s，运动过程中始终保持PQ∥AC，直线PQ交AB于点P、交BC于点Q、交BD于点F．连接PM，设运动时间为t秒 （0＜t＜5）．
（1）当t为何值时，四边形PQCM是平行四边形？
（2）设四边形PQCM的面积为ycm²，求y与t之间的函数关系式；
（3）是否存在某一时刻t，使S_{四边形PQCM}＝S_△ABC？若存在，求出t的值；若不存在，说明理由；
（4）连接PC，是否存在某一时刻t，使点M在线段PC的垂直平分线上？若存在，求出此时t的值；若不存在，说明理由．

如图，在平面直角坐标系中，直线AB与x轴、y轴分别交于点A、B，直线CD与x轴、y轴分别交于点C、D，AB与CD相交于点E，线段OA、OC的长是一元二次方程－18x+72=0的两根（OA＞OC），BE=5，tan∠ABO=．

（1）求点A，C的坐标；
（2）若反比例函数y=的图象经过点E，求k的值；
（3）若点P在坐标轴上，在平面内是否存在一点Q，使以点C，E，P，Q为顶点的四边形是矩形？若存在，请写出满足条件的点Q的个数，并直接写出位于x轴下方的点Q的坐标；若不存在，请说明理由．