在形如 的式子中,我们已经研究过两种情况:①已知a和b,求N,这是乘方运算;②已知b和N,求a,这是开方运算;
的式子中,我们已经研究过两种情况:①已知a和b,求N,这是乘方运算;②已知b和N,求a,这是开方运算;
现在我们研究第三种情况:已知a和N,求b,我们把这种运算叫做对数运算。
定义:如果 (a>0,a≠1,N>0),则b叫做以a为底N的对数,记作:
(a>0,a≠1,N>0),则b叫做以a为底N的对数,记作: ,例如:求
,例如:求 ,因为
,因为 =8,所以
=8,所以 =3;又比如∵
=3;又比如∵ ,∴
,∴ .
.根据定义计算:(本小题6分)
① =____;②
=____;② = ;
= ;
③如果 ,那么x= 。
,那么x= 。设
 则
则 (a>0,a≠1,M、N均为正数),
(a>0,a≠1,M、N均为正数),
∵ ,∴
,∴ ∴
∴ ,
,
即
这是对数运算的重要性质之一,进一步,我们还可以得出: = .(其中M1、M2、M3、……、Mn均为正数,a>0,a≠1)(本小题2分)
= .(其中M1、M2、M3、……、Mn均为正数,a>0,a≠1)(本小题2分)请你猜想:
 (a>0,a≠1,M、N均为正数).(本小题2分)
(a>0,a≠1,M、N均为正数).(本小题2分)
下列各题中的数据,哪个是精确值? ( )
| A.客车在公路上的速度是60km/h |
| B.我们学校大约有1000名学生 |
| C.小明家离学校距离是3km |
| D.从学校到火车站共有10个红灯路口 |
妈妈让小明给客人烧水沏茶,洗开水壶要用1分钟,烧开水要用15分钟,洗茶壶要用1分钟,洗茶杯要用1分钟,放茶叶要用2分钟,给同学打电话要用1分钟.为使客人早点喝上茶,小明最快可在几分钟内完成这些工作?
| A.19分钟 | B.18分钟 | C.17分钟 | D.16分钟 |
甲、乙两地相距20千米.小明上午8:30骑自行车由甲地去乙地,平均车速8千米/小时;小丽上午10:00坐公共汽车沿相同的路线也由甲地去乙地,平均车速为40千米/小时.
(1)分别写出两人离甲地的距离与时间的函数关系式,并在同一平面直角坐标系中画出两个函数的图象;
(2)判断谁先到达乙地,并说明理由.
黄石市2011年6月份某日一天的温差为11℃,最高气温为t℃,则最低气温可表示为( )
| A.(11+t)℃ | B.(11﹣t)℃ | C.(t﹣11)℃ | D.(﹣t﹣11)℃ |
爱动脑筋的小明制造了一个小黑匣,只要你输入一个数字,它就输出另一个数来,好奇心强的小亮赶紧试试了一下,结果得到了下面的表格
| 输入 |
2 |
5 |
10 |
17 |
26 |
37 |
… |
| 输出 |
1 |
… |
聪明的你一定知道当输入的数是65时,输出的结果是
某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2:1.在温室内,沿前侧内墙保留3m宽的空地,其它三侧内墙各保留1m宽的通道.当矩形温室的长与宽各为多少时,蔬菜种植区域的面积是288m2?
某一工程,在工程招标时,接到甲、乙两个工程队的投标书.施工一天,需付甲工程队工程款1.2万元,乙工程队工程款0.5万元.工程领导小组根据甲、乙两队的投标书测算,有如下方案:甲队单独完成这项工程刚好如期完成,乙队单独完成这项工程要比规定日期多用6天。这项工程工期是多少天?
若甲、乙两队合做3天,余下的工程由乙队单独做也正好如期完成.
试问:在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由
下列命题是真命题的是( )
| A.相等的角是对顶角 |
| B.两直线被第三条直线所截,内错角相等 |
C.若 ,则 ,则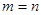 |
| D.有一角对应相等的两个菱形相似 |
如图,大楼AB、CD和大树EF的底端B、D、F在同一直线上,BF=FD=10米,AB=16米,某人在楼顶A处测得点C的仰角为22°,测得点E的俯角为45°.(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)
(1)求大树EF的高度;
(2)求大楼CD的高度.
我国从2008年6月1日起执行“限塑令”.“限塑令”执行前,某校为了了解本校学生所在家庭使用塑料袋的数量情况,随机调查了10名学生所在家庭月使用塑料袋的数量,结果如下(单位:只):
65,70,85,75,85,79,74,91,81,95.
(1)计算这10名学生所在家庭平均月使用塑料袋多少只?
(2)“限塑令”执行后,家庭月使用塑料袋数量预计将减少50%.根据上面的计算结果,估计该校1 000名学生所在家庭月使用塑料袋可减少多少只?
我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段 的最小覆盖圆就是以线段
的最小覆盖圆就是以线段 为直径的圆.
为直径的圆.
(1)请分别作出图1中两个三角形的最小覆盖圆(要求用尺规作图,保留作图痕迹,不写作法);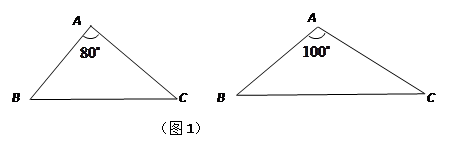
(2)探究三角形的最小覆盖圆有何规律?请写出你所得到的结论(不要求证明);
(3)某地有四个村庄 (其位置如图2所示),现拟建一个电视信号中转站,为了使这四个村庄的居民都能接收到电视信号,且使中转站所需发射功率最小(距离越小,所需功率越小),此中转站应建在何处?请说明理由.
(其位置如图2所示),现拟建一个电视信号中转站,为了使这四个村庄的居民都能接收到电视信号,且使中转站所需发射功率最小(距离越小,所需功率越小),此中转站应建在何处?请说明理由.