如图,河边有一条笔直的公路 ,公路两侧是平坦的草地.在数学活动课上,老师要求测量河对岸
,公路两侧是平坦的草地.在数学活动课上,老师要求测量河对岸 点到公路的距离,请你设计一个测量方案.要求:
点到公路的距离,请你设计一个测量方案.要求:
(1)列出你测量所使用的测量工具;
(2)画出测量的示意图,写出测量的步骤;
(3)用字母表示测得的数据,求出 点到公路的距离.
点到公路的距离.
如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1,A2,A3,A4,…表示,则顶点A55的坐标是( )
| A.(13,13) | B.(-13,-13) | C.(14,14) | D.(-14,-14) |
如图,将边长为1的等边△PQR沿着边长为1的正五边形ABCDE外部的边连续滚动(点Q、点R分别与点A、点B重合),当△PQR第一次回到原来的起始位置时(顶点位置与原来相同),点P所经过的路线长为 ( )
A. B.
B.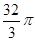 C.
C.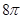 D.
D.
小明家准备建造长为28米的蔬菜大棚,示意图如图(1).它的横截面为如图(2)所示的四边形 ,已知
,已知 米,
米, 米,
米, ,
, ,
, 到
到 的距离
的距离 为1米.矩形棚顶
为1米.矩形棚顶 及矩形
及矩形 由钢架及塑料薄膜制作,造价为每平方米120元,其它部分(保温墙体等)造价共9250元,则这个大棚的总造价为多少元?(精确到1元)
由钢架及塑料薄膜制作,造价为每平方米120元,其它部分(保温墙体等)造价共9250元,则这个大棚的总造价为多少元?(精确到1元)
(下列数据可供参考 )
)
(本题8分)有这样的一道题:“计算: 的值,其中x=2010”.甲同学把“x=2010”错抄成“x=2001”,但他的计算结果也是正确的。你说这是怎么回事?
的值,其中x=2010”.甲同学把“x=2010”错抄成“x=2001”,但他的计算结果也是正确的。你说这是怎么回事?
晚上,小亮走在大街上.他发现:当他站在大街两边的两盏路灯之间,并且自己被两边路灯照在地上的两个影子成一直线时,自己右边的影子长为3米,左边的影子长为1.5米.又知自己身高1.80米,两盏路灯的高相同,两盏路灯之间的距离为12米,则路灯的高为 米.
如图,已知抛物线y=x2+bx-3a过点A(1,0),B(0,-3),与x轴交于另一点C.
(1)求抛物线的解析式;
(2)若在第三象限的抛物线上存在点P,使△PBC为以点B为直角顶点的直角三角形,
求点P的坐标;
(3)在(2)的条件下,在抛物线上是否存在一点Q,使以P,Q,B,C为顶点的四边形
为直角梯形?若存在,请求出点Q的坐标;若不存在,请说明理由.
如图,在靠墙(墙长为18m)的地方围建一个矩形的养鸡场,另三边用竹篱笆围成,如果竹篱笆总长为35m,求鸡场的长y (m)与宽x (m)的函数关系式,并求自变量的取值范围。
某校数学课题学习小组在“测量教学楼高度”的活动中,设计了以下两种方案:
| 课题 |
测量教学楼高度 |
|
| 方案 |
一 |
二 |
| 图示 |
 |
 |
| 测得数据 |
CD=6.9m,∠ACG=22°,∠BCG=13°, |
EF=10m,∠AEB=32°,∠AFB=43° |
| 参考数据 |
sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin13°≈0.22,cos13°≈0.97,tan13°≈0.23 |
sin32°≈0.53,cos32°≈0.85,tan32°≈0.62 sin43°≈0.68,cos43°≈0.73,tan43°≈0.93 |
请你选择其中的一种方法,求教学楼的高度(结果保留整数)
小芬买15份礼物,共花了900元,已知每份礼物内鄱有1包饼干及每支售价20元的棒棒糖2支,若每包饼干的售价为x元,则依题意可列出下列哪一个一元一次方程式?
( )
| A.15(2x+20)=900 | B.15x+20´2=900 |
| C.15(x+20´2)=900 | D.15´x´2+20=900 |
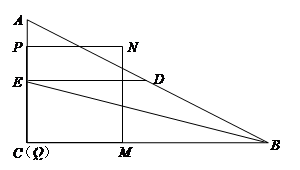
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=12,D、E分别为边AB、AC的中点,连结DE,点P从点A出发,沿折线AE-ED-DB运动,到点B停止.点P在折线AE-ED上以每秒1个单位的速度运动,在DB上以每秒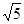 个单位的速度运动. 过点P作PQ⊥BC于点Q,以PQ为边在PQ右侧作正方形PQMN,使点M落在线段BC上.设点P的运动时间为
个单位的速度运动. 过点P作PQ⊥BC于点Q,以PQ为边在PQ右侧作正方形PQMN,使点M落在线段BC上.设点P的运动时间为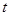 秒(
秒(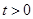 ).
).
(1)在整个运动过程中,求正方形PQMN的顶点N落在AB边上时对应的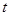 的值;
的值;
(2)连结BE,设正方形PQMN与△BED重叠部分图形的面积为S,请直接写出S与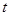 之间的函数关系式和相应的自变量
之间的函数关系式和相应的自变量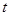 的取值范围;
的取值范围;
(3)当正方形PQMN顶点P运动到与点E重合时,将正方形PQMN绕点Q逆时针旋转60°得正方形
P1 Q M1 N1,问在直线DE与直线AC上是否存在点G和点H,使△GHP1是等腰直角三角形? 若
存在,请求出EG的值;若不存在,请说明理由.
1883年,康托尔构造的这个分形,称做康托尔集.从数轴上单位长度线段开始,康托尔取走其中间三分之一而达到第一阶段;然后从每一个余下的三分之一线段中取走其中间三分之一而达到第二阶段.无限地重复这一过程,余下的无穷点集就称做康托尔集.上图是康托尔集的最初几个阶段,当达到第八个阶段时,余下的所有线段的长度之和为 .
如图中,每个图形都是若干个棋子围成的正方形图案,图案的每条边(包括两个顶点)上都有n(n≤2)个棋子,每个图案的棋子总数为S,按图的排列规律推断S与n之间的关系可以用式子___________来表示. 
某厂投入200 000元购置生产某新型工艺品的专用设备和模具,共生产这种工艺品 件,又知生产每件工艺品还需投入350元,每件工艺品以销售价550元全部售出,生产这
件,又知生产每件工艺品还需投入350元,每件工艺品以销售价550元全部售出,生产这 件工艺品的销售利润=销售总收入-总投入,则下列说法错误的是( )
件工艺品的销售利润=销售总收入-总投入,则下列说法错误的是( )
A.若产量 ,则销售利润为负值; ,则销售利润为负值; |
B.若产量 ,则销售利润为零; ,则销售利润为零; |
C.若产量 ,则销售利润为 ,则销售利润为 元; 元; |
D.若产量 ,则销售利润随着产量 ,则销售利润随着产量 的增大而增加 的增大而增加 |