初中数学应用类问题解答题

李老师在与同学进行“蚂蚁怎样爬最近”的课题研究时设计了以下三个问题，请你根据下列所给的重要条件分别求出蚂蚁需要爬行的最短路程的长。

（1）如图1，正方体的棱长为5cm一只蚂蚁欲从正方体底面上的点A沿着正方体表面爬到点C1处；
（2）如图2，圆锥的母线长为4cm，底面半径r=cm，一只蚂蚁欲从圆锥的底面上的点A出发，沿圆锥侧面爬行一周回到点A．
(3)如图3，是一个没有上盖的圆柱形食品盒，一只蚂蚁在盒外表面的A处，它想吃到
盒内表面对侧中点B处的食物，已知盒高10cm，底面圆周长为32cm，A距下底面3cm

有一木质圆形脸谱工艺品，H、T两点为脸谱的耳朵，打算在工艺品反面两耳连线中点D处打一小孔，现在只有一块无刻度单位的直角三角板（斜边大于工艺品的直径），请你用两种不同的方法确定D点的位置，并分别说明理由（图中点O为圆心）

某化妆品公司每月付给销售人员的工资有两种方案．
方案一：没有底薪，只拿销售提成；方案二：底薪加销售提成．
设x（件）是销售商品的数量，y（元）是销售人员的月工资．如图所示，y1为方案一的函数图象，y2为方案二的函数图象．已知每件商品的销售提成方案二比方案一少7元．从图中信息解答如下问题
（注：销售提成是指从销售每件商品得到的销售额中提取一定数量的费用）：

（1）求y1的函数解析式；
（2）请问方案二中每月付给销售人员的底薪是多少元？
（3）如果该公司销售人员小丽的月工资要超过1000元，那么小丽选用哪种方案最好？至少要销售商品多少件？

2008年7月，育英中学举办迎奥运绘画展，小鹏所绘长为90cm，宽为40cm的图画被选中去参加展览，图画四周加上等宽的金边装裱制成挂图后，图画的面积是整个挂图面积的72%，你知道金边有多宽吗？

如图6,直升飞机在资江大桥AB的上方P点处，此时飞机离地面的高度PO=450米，且A、B、O三点在一条直线上，测得大桥两端的俯角分别为α=30°，β=45°，求大桥的长AB．

如图5，初三（1）班课外活动小组利用标杆测量学校旗杆的高度，已知标杆高度，标杆与旗杆的水平距离，人的眼睛与地面的高度，人与标杆的水平距离，求旗杆的高度.

某校欲招聘一名数学教师，学校对甲、乙、丙三位候选人进行了三项能力测试，各项测试成绩满分均为100分，根据结果择优录用．三位候选人的各项测试成绩如下表所示：

测试项目	测试成绩
甲	乙	丙
教学能力	85	73	73
科研能力	70	71	65
组织能力	64	72	84

 
（1）如果根据三项测试的平均成绩，谁将被录用，说明理由；
（2）根据实际需要，学校将教学、科研和组织三项能力测试得分按5∶3∶2的比例确定每人的成绩，谁将被录用，说明理由

如图，为了测量池塘的宽度DE，在池塘周围的平地上选择了A、B、C三点，且A、D、E、C四点在同一条直线上，∠C=90°，已测得AB=100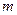，BC=60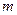，AD=20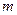，EC=10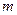，求池塘的宽度DE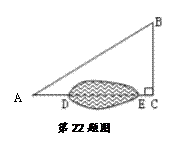

图形的操作过程（本题中四个矩形的水平方向的边长均为a，竖直方向的边长均b）：

●在图1中，将线段A1A2向右平移1个单位到B1B2，得到封闭图形A1A2B2B1（即阴影部分）；
●在图2中，将折线A1A2A3向右平移1个单位到B1B2B3，得到封闭图形A1A2A3B3B2B1（即阴影部分）．
（1）在图3中，请你类似地画一条有两个折点的线，同样向右平移1个单位，从而得到一个封闭图形，并用斜线画出阴影；
（2）请你分别写出上述三个图形中除去阴影部分后剩余部分的面积：
S1＝__________，S2＝__________，S3＝__________．
（3）联想与探索
 
如上图，在一块矩形草地上，有一条弯曲的柏油小路（小路任何地方的水平宽度都是1个单位），请你猜想空白部分表示的草场地面积是多少？并说明你的猜想是正确的．

如图，一艘渔政船从小岛A处出发，向正北方向以每小时20海里的速度行驶了1.5小时到达B处执行任务，再向正东方向以相同的速度行驶了2小时到达C处继续执行任务，然后以相同的速度直接从C处返回A处.

（1）分别求AB、 BC的长；
（2）问返回时比出去时节省了多少时间？

如图，某校有一块长为(3a＋b)米，宽为(2a+b)米的长方形地块，学校计划将阴影部分进行绿化，中间将修建一座雕像.

(1) 用含a、b的代数式表示绿化面积；
(2) 求出当a=3米,b=2米时的绿化面积．

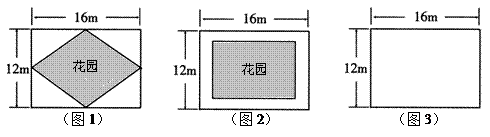
在一块长16m，宽12m的矩形荒地上，要建造一个花园，要求花园面积是荒地面积的一半，且整体图案成轴对称图形．下面是小华、小芳与小明的设计方案.


请你根据以上的对话，完成下列问题.
（1）你认为小华所设计的花园的形状是    ，整个设计图案共有   条对称轴；
(2)请你帮助小芳计算出道路的宽度的值；
（3）请你根据小明的设计方案在图3中画出符合设计条件的草图，然后根据你所画的草图求出该等腰梯形的上底和下底的长.

某高铁工程即将动工,工程需要测量某一条河的宽度.如图，一测量员在河岸边的A处测得对岸岸边的一根标杆B在它的正北方向，测量员从A点开始沿岸边向正东方向前进100米到达点C处，测得标杆B在北偏西280处.求河宽AB.（结果精确到1米）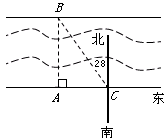

如图1，已知直线的解析式为,它与轴、y轴分别相交于A、B两点．点C从点O出发沿OA以每秒1个单位的速度向点A匀速运动；点D从点A出发沿AB以每秒1个单位长的速度向点B匀速运动，点C、D同时出发，当点C到达点A时同时停止运动．伴随着C、D的运动，EF始终保持垂直平分CD，垂足为E，且EF交折线AB-BO-AO于点F．

(1)直接写出A、B两点的坐标；
(2) 设点C、D的运动时间是t秒（t＞0）．
①用含t的代数式分别表示线段AD和AC的长度；
②在点F运动的过程中，四边形BDEF能否成为直角梯形？若能求t的值；若不能，请说明理由．(可利用备用图解题)

请你观察思考下列计算过程：
∵，∴；
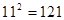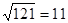同样：∵，∴；……………………………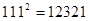
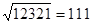由此猜想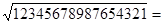                。