如图①,在矩形 ABCD中,AB=10cm,BC=8cm.点P从A出发,沿A→B→C→D路线运动,到D停止;点Q从D出发,沿 D→C→B→A路线运动,到A停止.若点P、点Q同时出发,点P的速度为每秒1cm,点Q的速度为每秒2cm,a秒时点P、点Q同时改变速度,点P的速度变为每秒bcm,点Q的速度变为每秒dcm.图②是点P出发x秒后△APD的面积S1(cm2)与x(秒)的函数关系图象;图③是点Q出发x秒后△AQD的面积S2(cm2)与x(秒)的函数关系图象.


(1)参照图象,求b、图②中c及d的值;
(2)连接PQ,当PQ平分矩形ABCD的面积时,运动时间x的值为 ;
(3)当两点改变速度后,设点P、Q在运动线路上相距的路程为y(cm),求y(cm)与运动时间x(秒)之间的函数关系式,并写出自变量x的取值范围;
(4)若点P、点Q在运动路线上相距的路程为25cm,求x的值.
做服装生意的王老板经营甲、乙两个店铺,每个店铺在同一段时间内都能售出A、B两种款式的服装合计30件,并且每售出一件A款式和B款式服装,甲店铺获利润分别为30元和35元,乙店铺获利润分别为26元和36元.某日,王老板进A款式服装36件,B款式服装24件,并将这批服装分配给两个店铺各30件.
(1)怎样将这60件服装分配给两个店铺,能使两个店铺在销售完这批服装后所获利润相同?
(2)怎样分配这60件服装能保证在甲店铺获利润不小于950元的前提下,王老板获利的总利润最大?最大的总利润是多少?
如图,一艘科学考察船由港口A出发沿正北方向航行,在航线的一侧有两个小岛C、D.考察船在A处时,测得小岛C在船的正西方,小岛D在船的北偏西30°方向.考察船向北航行了12千米到B处时,测得小岛C在船的南偏西30°方向,小岛D在船的南偏西60°方向.求小岛C、D之间的距离.
如图,将边长为1的等边△PQR沿着边长为1的正五边形ABCDE外部的边连续滚动(点Q、点R分别与点A、点B重合),当△PQR第一次回到原来的起始位置时(顶点位置与原来相同),点P所经过的路线长为 ( )
A. B.
B.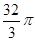 C.
C.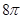 D.
D.
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=12,D、E分别为边AB、AC的中点,连结DE,点P从点A出发,沿折线AE-ED-DB运动,到点B停止.点P在折线AE-ED上以每秒1个单位的速度运动,在DB上以每秒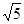 个单位的速度运动. 过点P作PQ⊥BC于点Q,以PQ为边在PQ右侧作正方形PQMN,使点M落在线段BC上.设点P的运动时间为
个单位的速度运动. 过点P作PQ⊥BC于点Q,以PQ为边在PQ右侧作正方形PQMN,使点M落在线段BC上.设点P的运动时间为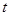 秒(
秒(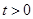 ).
).
(1)在整个运动过程中,求正方形PQMN的顶点N落在AB边上时对应的 的值;
的值;
(2)连结BE,设正方形PQMN与△BED重叠部分图形的面积为S,请直接写出S与 之间的函数关系式和相应的自变量
之间的函数关系式和相应的自变量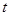 的取值范围;
的取值范围;
(3)当正方形PQMN顶点P运动到与点E重合时,将正方形PQMN绕点Q逆时针旋转60°得正方形
P1 Q M1 N1,问在直线DE与直线AC上是否存在点G和点H,使△GHP1是等腰直角三角形? 若
存在,请求出EG的值;若不存在,请说明理由.
某蔬菜店第一次用800元购进某种蔬菜,由于销售状况良好,该店又用1400元第二次购进该品种蔬
菜,所购数量是第一次购进数量的2倍,但进货价每千克少了0.5元.
(1)第一次所购该蔬菜的进货价是每千克多少元?
(2)蔬菜店在销售中,如果两次售价均相同,第一次购进的蔬菜有3% 的损耗,第二次购进的蔬菜有5% 的损耗,若该蔬菜店售完这些蔬菜获利不低于1244元,则该蔬菜每千克售价至少为多少元?
小明在路灯AB下玩耍时发现自己的影长DF的长是3米,沿着BD方向来到点F处再测得自己的影长FG是4米.如果小明的身高是1.8米,求路灯AB的高度.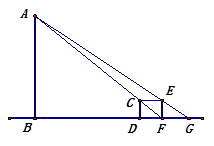
如图,旗杆AB的影子一部分在地面上,另一部分在某一建筑的墙上,小亮测得旗杆AB在地面上的影长BD为9.6 m,在墙面上的影长CD为2 m,同一时刻,小亮又测得竖立于地面1 m长的标杆的影长为1.2 m,请帮助小亮求出旗杆AB的高度.解: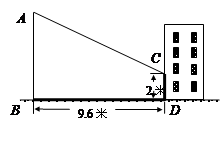
如图, 城气象台测得台风中心在
城气象台测得台风中心在 城的正西方
城的正西方 千米的
千米的 处,以每小时
处,以每小时 千米的速度向北偏东
千米的速度向北偏东 的
的 方向移动,距台风中心
方向移动,距台风中心 千米的范围内是受这次台风影响的区域.问
千米的范围内是受这次台风影响的区域.问 城是否会受到这次台风的影响?为什么?如果会受到影响,求出
城是否会受到这次台风的影响?为什么?如果会受到影响,求出 城遭受这次台风影响持续的时间.
城遭受这次台风影响持续的时间.
某市为治理污水,需要铺设一段全长为 的污水排放管道,为了尽量减少施工对城市交通所造成的影响,实际施工时每天的工效比原计划增加
的污水排放管道,为了尽量减少施工对城市交通所造成的影响,实际施工时每天的工效比原计划增加 ,结果提前
,结果提前 天完成这一任务,实际每天铺设多长管道?
天完成这一任务,实际每天铺设多长管道?
 年
年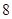 月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图所示),如果大正方形的面积是
月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图所示),如果大正方形的面积是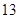 ,小正方形的面积是
,小正方形的面积是 ,直角三角形的较短直角边为
,直角三角形的较短直角边为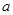 ,较长直角边为
,较长直角边为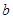 ,那么
,那么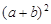 的值为( )
的值为( )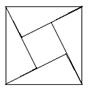
A.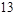 |
B.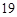 |
C.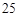 |
D.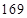 |
在一次400米比赛中,有如下的判断:甲说:丙第一,我第三;乙说:我第一,丁第四;丙说:丁第二,我第三.结果是每人的两句话中都只说对了一句,则可判断第一名是
| A.甲 | B.乙 | C.丙 | D.丁 |
如图,在梯形纸片ABCD中,BC∥AD,∠A+∠D=90°,tanA=2,过点B作BH⊥AD与H,BC=BH=2.动点 从点
从点 出发,以每秒1个单位的速度沿
出发,以每秒1个单位的速度沿 运动到点
运动到点 停止,在运动过程中,过点
停止,在运动过程中,过点 作
作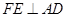 交折线
交折线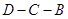 于点
于点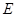 ,将纸片沿直线
,将纸片沿直线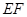 折叠,点
折叠,点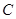 、
、 的对应点分别是点
的对应点分别是点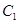 、
、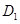 。设
。设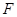 点运动的时间是
点运动的时间是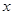 秒(
秒(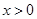 )。
)。
(1)当点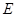 和点
和点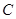 重合时,求运动时间
重合时,求运动时间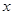 的值;
的值;
(2)在整个运动过程中,设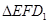 或四边形
或四边形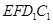 与梯形
与梯形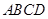 重叠部分面积为
重叠部分面积为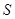 ,请直接写出
,请直接写出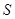 与
与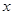 之间的函数关系式和相应自变量
之间的函数关系式和相应自变量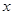 的取值范围;
的取值范围;
(3)平移线段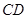 ,交线段
,交线段 于点
于点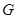 ,交线段
,交线段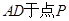 。在直线
。在直线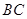 上存在点
上存在点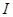 ,使
,使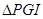 为等腰直角三角形。请求出线段
为等腰直角三角形。请求出线段 的所有可能的长度。
的所有可能的长度。
在平面直角坐标系中,△ABC的位置如图所示,请解答下列问题:
(1)将△ABC向下平移3个单位长度,得到△A1B1C1,画出平移后的△A1B1C1;
(2)将△ABC绕点O顺时针方向旋转180°,得到△A2B2C2,画出旋转后的△A2B2C2,并写出A2点的坐标.
某通讯器材公司销售一种市场需求较大的新型通讯产品.已知每件产品的进价为40元,每年销售该种产品的总开支(不含进价)总计120万元.在销售过程中发现,年销售量 (万件)与销售单位
(万件)与销售单位 (元)之间存在着如图所示的一次函数关系.
(元)之间存在着如图所示的一次函数关系.
(1)求 关于
关于 的函数关系式;
的函数关系式;
(2)试写出该公司销售该种产品的年获利 (万元)关于销售单价
(万元)关于销售单价 (元)的函数关系式(年获利=年销售额-年销售产品总进价-年总开支).当销售单价
(元)的函数关系式(年获利=年销售额-年销售产品总进价-年总开支).当销售单价 为何值时,年获利最大?并求这个最大值;
为何值时,年获利最大?并求这个最大值;
(3)若公司希望该种产品一年的销售获利不低于40万元,借助(2)中函数的图象,请你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?