如图，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上．已知纸板的两条直角边DF=50cm，EF=30cm，测得边DF离地面的高度AC=1.5m，CD=20m，则树高AB为（ ）
| A．12 m | B．13.5 m | C．15 m | D．16.5 m |
小明沿着坡比为1：
的山坡向上走了600m，则他升高了（ ）
A． m |
B．200 m |
C．300 m | D．200m |
把一块直尺与一块三角板如图放置，若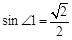
，则∠2的度数为（ ）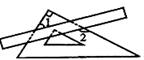
| A．120° | B．135° | C．145° | D．150° |
（本题10分）
在向红星镇居民介绍王家庄位置的时候，我们可以这样说:如图，在以红星镇为原点，正东方向为x轴正方向，正北方向为y轴正方向的平面直角坐标系（1单位长度表示的实际距离为1km）中，王家庄的坐标为（5，5）；也可以说，王家庄在红星镇东北方向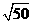
km的地方。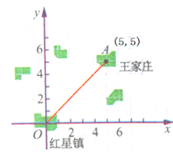
还有一种方法广泛应用于航海、航空、气象、军事等领域。如右下图：在红星镇所建的雷达站O的雷达显示屏上，把周角每15°分成一份，正东方向为0°，相邻两圆之间的距离为1个单位长度（1单位长度表示的实际距离为1km），现发现2个目标，我们约定用（10，15°）表示点M在雷达显示器上的坐标，则：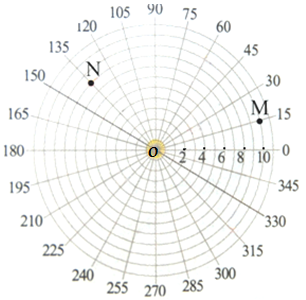
（1）点N可表示为 ；王家庄位置可表示为 ；点N关于雷达站点0成中心对称的点P的坐标为 ；
（2）S△OMP= ；
（3）若有一家大型超市A在图中（4，30°）的地方，请直接标出点A，并将超市A与雷达站O连接，现准备在雷达站周围建立便民服务店B，使得△ABO为底角30°的等腰三角形，请直接写出B点在雷达显示屏上的坐标.
（本题9分）甲、乙两地距离300km，一辆货车和一辆轿车先后从甲地出发驶向乙地．如图，线段OA表示货车离甲地的距离y（km）与时间x（h）之间的函数关系，折线BCDE表示轿车离甲地的距离y（km）与时间x（h）之间的函数关系，根据图象，解答下列问题：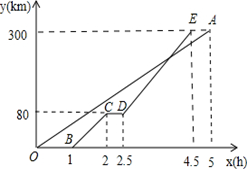
（1）请你在A，B，C，D，E五个点任意选择一个点解释它的实际意义；
（2）求线段DE对应的函数关系式；
（3）当轿车出发1h后，两车相距多少千米；
（4）当轿车出发几小时后两车相距30km？
（本题8分）如图，在梯形ABCD中，AD//BC，E是AD的中点，BC=5，AD=12，梯形高为4，∠A =45°，P为AD边上的动点.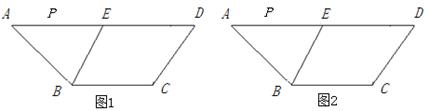
（1）当PA的值为____________时，以点P、B、C、E为顶点的四边形为直角梯形；
（2）当PA的值为____________时，以点P、B、C、E为顶点的四边形为平行四边形；
（3）点P在AD边上运动的过程中，以P、B、C、E为顶点的四边形能否构成菱形？如果能，求出PA长．如果不能，也请说明理由.
（本题8分）如图，四边形ABCD是矩形,点O在矩形上方，点B绕着点O逆时针旋转
后的对应点为点C．
（1）画出点A绕着点O逆时针旋转后的对应点E；
（2）连接CE,证明：CO平分∠ECD
（3）在（1）（2）的条件下，连接ED,猜想ED与CO的位置关系，并证明你的结论.
（本题8分）阅读下面材料，再回答问题：
有一些几何图形可以被某条直线分成面积相等的两部分，我们将“把一个几何图形分成面积相等的两部分的直线叫做该图形的二分线”，如：圆的直径所在的直线是圆的“二分线”，正方形的对角线所在的直线是正方形的“二分线”.
解决下列问题：
（1）菱形的“二分线”是 ；
（2）三角形的“二分线”是 ；
（3）在下图中，试用两种不同的方法分别画出等腰梯形ABCD的“二分线”,简述做法.
图1 图2
（本题7分）小明本学期的数学成绩如下表所示：
| 测验类别 |
平时 |
a |
b |
c |
|||
| 测试1 |
测试2 |
测试3 |
测试4 |
平时平均数 |
期中考试 |
期末考试 |
|
| 成绩 |
108 |
103 |
101 |
108 |
|
110 |
114 |
（1）六次考试的中位数和众数分别是什么？
（2）请计算小明该学期的数学平时平均成绩；
（3）如果学期的总评成绩是根据如图所示的比例计算所得，已知小明该学期的数学总评成绩为111分，请计算出总评成绩中期中、期末成绩各自所占的比例．
甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米，先到终点的人原地休息．已知甲先出发2秒．在跑步过程中，甲、乙两人的距离y（米）与乙出发的时间t（秒）之间的关系如图所示，给出以下结论：①a=8；②b=92；③c=123．其中正确的是
| A．①②③ | B．仅有①② | C．仅有①③ | D．仅有②③ |
(10分) 某通讯公司推出①、②两种手机通话月收费方式供用户选择，其中一种有月租费，另一种无月租费，且两种收费方式的月通话时间x（分钟）与收费y（元）之间的函数关系如图所示．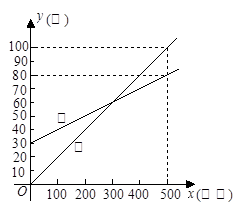
（1）有月租费的收费方式是 （填①或②），月租费是 元；
（2）分别求出①，②两种收费方式中y与自变量x之间的函数关系式；
（3）请你根据用户月通话时间的多少，给出经济实惠的选择建议
2012年5月18日，某国3艘炮艇追袭5条中国渔船．刚刚完成黄岩岛护渔任务的“中国渔政310”船人船未歇立即追往北纬11度22分、东经110度45分附近海域护渔，保护100多名中国渔民免受财产损失和人身伤害．某国炮艇发现中国目前最先进的渔政船正在疾速驰救中国渔船，立即掉头离去．
解决问题：如图，已知“中国渔政310”船（A）接到陆地指挥中心（B）命令时，渔船（C）位于陆地指挥中心正南方向，位于“中国渔政310”船西南方向，“中国渔政310”船位于陆地指挥中心南偏东60°方向，AB=
海里，“中国渔政310”船最大航速20海里/时．根据以上信息，请你求出“中国渔政310”船赶往出事地点需要多少时间．
在开展“学雷锋社会实践”活动中，某校为了解全校1200名学生参加活动的情况，随机调查了50名学生每人参加活动的次数，并根据数据绘成条形统计图如下：
（1）求这50个样本数据的平均数、众数和中位数；
（2）根据样本数据，估算该校1200名学生共参加了多少次活动．
如图甲所示，在直角梯形ABCD中，AB∥DC，
．动点P从点B出发，沿梯形的边由B→C→D→A运动．设点P运动的路程为x，△ABP的面积为y．把y看作x的函数，函数的图像如图乙所示，则△ABC的面积为( ) 
| A．10 | B．16 | C．18 | D．32 |
如图，矩形的长和宽分别为8cm和4cm，截去一个宽为x的小矩形（阴影部分）后余下另一个矩形的面积S与x之间的关系可表示为（ ）．
| A．S＝4x | B．S＝4(8－x) | C．S＝8(4－x) | D．S＝8x |
粤公网安备 44130202000953号