初中数学有理数无理数的概念与运算解答题

把下列各数填在相应的表示集合的大括号内
-6， ， ，  3.14，  -0.4，  - 
，    0，    1.1010010001……
整 数{                                            ……}
无理数{                                            ……}
负分数{                                            ……}
负实数{                                            ……}

在数轴上近似地表示下列各数，并把这些数按从小到大顺序进行排列，用“＜”连接。
4， －1.5，  0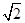， ， －π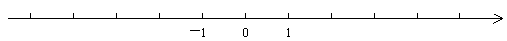

在一条东西走向的马路上，有少年宫、学校、商场、医院四家公共场所。已知少年宫在学校东300米，商场在学校西200米，医院在学校东500米。若将马路近似地看成一条直线，以学校为原点，向东方向为正方向，用1个单位长度表示100米。
(1)在数轴上表示出四家公共场所的位置；
(2)计算少年宫与商场之间的距离。

10袋小麦以每袋150千克为标准，超过150千克的部分记为正数，不足150千克的部分记为负数，记录情况如下表：

编号	1	2	3	4	5	6	7	8	9	10
差值/kg	-6	-3	-1	+7	+3	+4	-3	-2	-2	+1

（1）与标准重量相比较，10袋小麦总计超过或不足多少千克？
（2）每袋小麦的平均重量是多少千克？

计算题        （2）
    （4）

问题：你能比较两个数2012²⁰¹³和2013²⁰¹²的大小吗？
为了解决这个问题，我们先把它抽象成数学问题，写出它的一般形式，即比较nⁿ⁺¹和(n+1)ⁿ的大小（n是自然数），然后我们从分析n="1,n=2,n=3,……" 这些简单情形入手，从中发现规律，经过归纳，猜想出结论．
（1）通过计算，比较下列各组中两个数的大小：
① 1²   2¹                      ② 2³   3² 
③ 3⁴   4³                      ④ 4⁵    5⁴  
⑤ 5⁶   6⁵             ⑥6⁷   7⁶
 ……
（2）从第（1）题的结果经过归纳，可以猜想出nⁿ⁺¹和(n+1)ⁿ （n≥3）的大小关系
式是                                                   
（3）根据上面归纳猜想得到的一般结论，试比较两个数的大小：
2012²⁰¹³       2013²⁰¹²   （填”>”,”<”, “=”）

计算
（1）            （2）(+－)×（－48）
（3）      （4）（结果精确到0.01）

      
（1）第5个式子等号右边应填的数是      ；
（2）根据规律填空1＋3＋5＋7＋…＋(2n-1)＝      ；
（3）计算：1＋3＋5＋7＋…＋2013 ＝      .

阅读下题的计算方法。
计算 。
解：原式=
=
=
=
上面这种解题方法叫做拆项法，按此方法计算：

某天早上，一辆交通巡逻车从A地出发，在东西向的马路上巡视，中午到达B地，如果规定向东行驶为正，向西行驶为负，行驶纪录如下。（单位：km）

第一次	第二次	第三次	第四次	第五次	第六次	第七次
			＋12			－10

（1）B地在A地哪个方向，与A地相距多少千米？
（2）巡逻车在巡逻过程中，离开A地最远是多少千米？
（3）若每km耗油0.3升，问共耗油多少升？

如图所示，根据有理数，在数轴上的对应点的位置填空。

（1）    0         （2）    0
（3）    0           （4）    0

已知：b是最小的正整数，且a、b满足，请回答问题:
（1）请直接写出a、b、c的值:
a=__________  b=__________   c  =__________；
（2）a、b、c所对应的点分别为A、B、C，点M是A、B之间的一个动点，其对应的数为m，请化简（请写出化简过程）；
（3）在（1）（2）的条件下，点A、B、C开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动，假设t秒钟过后，若点B与点C之间的距离表示为BC，点A与点B之间的距离表示为AB.请问：的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值.

把下列实数表示在数轴上，并比较它们的大小（用“＜”连接).
， ， ， ，-3，  1.5

请你先认真阅读材料：
计算（－）÷（一＋－）．
解法l：                                                          解法2：
（－）÷（一＋－）                   原式的倒数为：
=（－）÷[（＋）－（＋）]    （一＋－）÷（－）
=（－）÷（ － ）                           =（一＋－）×（－30）
=（－）÷                                              =－20＋3－5＋12
=－×3                                                            =（－20－5）＋（3＋12）
=－                                                                 =－10
故原式=－
再根据你对所提供材料的理解，选择合适的方法计算：
（一）÷（一＋－）．

请你做评委：在一堂数学活动课上，同在一合作学习小组的小明、小亮、小丁、小彭对刚学过的知识发表了自己的一些感受：
小明说：“绝对值不大于4的整数有7个。”
小丁说：“若=3，=2，则的值为5或1。”
小亮说：“＜，因为两个负数比较大小，绝对值大的数反而小。”
小彭说：“多项式是一次三项式。”
依次判断四位同学的说法是否正确，如不正确，请帮他们修正，写出正确的说法。