初中数学列表法与树状图法试题

端午节是我国传统佳节．小峰同学带了4个粽子（除粽馅不同外，其它均相同），其中有两个肉馅粽子、一个红枣馅粽子和一个豆沙馅粽子，准备从中任意拿出两个送给他的好朋友小悦．

（1）用树状图或列表的方法列出小悦拿到两个粽子的所有可能结果；

（2）请你计算小悦拿到的两个粽子都是肉馅的概率．

某校开展了"禁毒"知识的宣传教育活动．为了解这次活动的效果，现随机抽取部分学生进行知识测试，并将所得数据绘制成不完整的统计图表．

等级	频数（人数）	频率
优秀	60	0.6
良好	$a$	0.25
合格	10	$b$
基本合格	5	0.05
合计	$c$	1

根据统计图表提供的信息，解答下列问题：

（1） $a=$ 　　， $b=$ 　　， $c=$ 　　；

（2）补全条形统计图；

（3）该学校共有1600名学生，估计测试成绩等级在合格以上（包括合格）的学生约有多少人？

（4）在这次测试中，九年级（3）班的甲、乙、丙、丁四位同学的成绩均为"优秀"，现班主任准备从这四名同学中随机选取两名同学出一期"禁毒"知识的黑板报，请用列表法或画树状图法求甲、乙两名同学同时被选中的概率．

某校组织一项公益知识竞赛，比赛规定：每个班级由2名男生、2名女生及1名班主任老师组成代表队．但参赛时，每班只能有3名队员上场参赛，班主任老师必须参加，另外2名队员分别在2名男生和2名女生中各随机抽出1名．初三（1）班由甲、乙2名男生和丙、丁2名女生及1名班主任组成了代表队，求恰好抽到由男生甲、女生丙和这位班主任一起上场参赛的概率．（请用“画树状图”或“列表”或“列举”等方法给出分析过程）

2021年5月，菏泽市某中学对初二学生进行了国家义务教育质量检测，随机抽取了部分参加15米折返跑学生的成绩，学生成绩划分为优秀、良好、合格与不合格四个等级，学校绘制了如下不完整的统计图．根据图中提供的信息解答下列问题：

（1）请把条形统计图补充完整；

（2）合格等级所占百分比为 　　 $\%$ ；不合格等级所对应的扇形圆心角为 　　度；

（3）从所抽取的优秀等级的学生 $A$ 、 $B$ 、 $C\dots$ 中，随机选取两人去参加即将举办的学校运动会，请根据列表或画树状图的方法，求出恰好抽到 $A$ 、 $B$ 两位同学的概率．

某校4月份八年级的生物实验考查，有 $A$、 $B$、 $C$、 $D$四个考查实验，规定每位学生只参加其中一个实验的考查，并由学生自己抽签决定具体的考查实验．小明、小丽都参加了本次考查．

（1）小丽参加实验 $A$考查的概率是　　；

（2）用列表或画树状图的方法求小明、小丽都参加实验 $A$考查的概率．

为庆祝建党100周年，让同学们进一步了解中国科技的快速发展，东营市某中学九（1）班团支部组织了一次手抄报比赛．该班每位同学从 $A$ ．"北斗卫星"； $B$ ．" $5G$ 时代"； $C$ ．"东风快递"； $D$ ．"智轨快运"四个主题中任选一个自己喜欢的主题．统计同学们所选主题的频数，绘制成不完整的统计图，请根据统计图中的信息解答下列问题：

（1）九（1）班共有 　　名学生；

（2）补全折线统计图；

（3） $D$ 所对应扇形圆心角的大小为 　　；

（4）小明和小丽从 $A$ 、 $B$ 、 $C$ 、 $D$ 四个主题中任选一个主题，请用列表或画树状图的方法求出他们选择相同主题的概率．

有2部不同的电影 $A$、 $B$，甲、乙、丙3人分别从中任意选择1部观看．

（1）求甲选择 $A$电影的概率；

（2）求甲、乙、丙3人选择同1部电影的概率（请用画树状图的方法给出分析过程，并求出结果）．

箱子里放有2个黑球和2个红球，它们除颜色外其余都相同，现从箱子里随机摸出两个球，恰好为1个黑球和1个红球的概率是　　．

某区域为响应“绿水青山就是金山银山”的号召，加强了绿化建设．为了解该区域群众对绿化建设的满意程度，某中学数学兴趣小组在该区域的甲、乙两个片区进行了调查，得到如下不完整统计图．

请结合图中信息，解决下列问题：

（1）此次调查中接受调查的人数为　　人，其中“非常满意”的人数为　　人；

（2）兴趣小组准备从“不满意”的4位群众中随机选择2位进行回访，已知这4位群众中有2位来自甲片区，另2位来自乙片区，请用画树状图或列表的方法求出选择的群众均来自甲片区的概率．

某校为了解节能减排、垃圾分类等知识的普及情况，从该校2000名学生中随机抽取了部分学生进行调查，调查结果分为“非常了解“、“了解”、“了解较少”、“不了解”四类，并将调查结果绘制出以下两幅不完整的统计图．请根据统计图回答下列问题：

（1）本次调查的学生共有　　人，估计该校2000名学生中“不了解”的人数约有　　人．

（2）“非常了解”的4人中有 $A_1$， $A_2$两名男生， $B_1$， $B_2$两名女生，若从中随机抽取两人去参加环保知识竞赛，请用画树状图和列表的方法，求恰好抽到2名男生的概率．

学习习近平总书记关于生态文明建设重要讲话，牢固树立“绿水青山就是金山银山”的科学观，让环保理念深入到学校，某校张老师为了了解本班学生3月植树成活情况，对本班全体学生进行了调查，并将调查结果分为了三类： $A$：好， $B$：中， $C$：差．

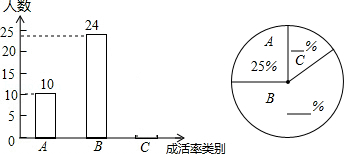
请根据图中信息，解答下列问题：

（1）求全班学生总人数；

（2）将上面的条形统计图与扇形统计图补充完整；

（3）张老师在班上随机抽取了4名学生，其中 $A$类1人， $B$类2人， $C$类1人，若再从这4人中随机抽取2人，请用画树状图或列表法求出全是 $B$类学生的概率．

箱子里放有2个黑球和2个红球，它们除颜色外其余都相同，现从箱子里随机摸出两个球，恰好为1个黑球和1个红球的概率是　　．

汤姆斯杯世界男子羽毛球团体赛小组赛比赛规则：两队之间进行五局比赛，其中三局单打，两局双打，五局比赛必须全部打完，赢得三局及以上的队获胜．假如甲，乙两队每局获胜的机会相同．

（1）若前四局双方战成 $2:2$，那么甲队最终获胜的概率是　　；

（2）现甲队在前两局比赛中已取得 $2:0$的领先，那么甲队最终获胜的概率是多少？

如图在三条横线和三条竖线组成的图形中，任选两条横线和两条竖线都可以围成一个矩形，从这些矩形中任选一个，则所选矩形含点 $A$ 的概率是 $($ 　　 $)$

A．

$\frac{1}{4}$

B．

$\frac{1}{3}$

C．

$\frac{3}{8}$

D．

$\frac{4}{9}$

为了倡导“节约用水，从我做起”，某市政府决定对该市直属机关200户家庭用水情况进行调查．市政府调查小组随机抽查了其中部分家庭一年的月平均用水量（单位：吨），调查中发现，每户家庭月平均用水量在 $3~7$吨范围内，并将调查结果制成了如下尚不完整的统计表：

月平均用水量（吨 $)$	3	4	5	6	7
频数（户数）	4	$a$	9	10	7
频率	0.08	0.40	$b$	$c$	0.14

请根据统计表中提供的信息解答下列问题：

（1）填空： $a=$　　， $b=$　　， $c=$　　．

（2）这些家庭中月平均用水量数据的平均数是 　　，众数是 　　，中位数是 　　．

（3）根据样本数据，估计该市直属机关200户家庭中月平均用水量不超过5吨的约有多少户？

（4）市政府决定从月平均用水量最省的甲、乙、丙、丁四户家庭中，选取两户进行“节水”经验分享．请用列表或画树状图的方法，求出恰好选到甲、丙两户的概率，并列出所有等可能的结果．