在四张背面完全相同的纸牌A、B、C、D,其中正面分别画有四个不同的几何图形(如图),小华将这4张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸一张.
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A、B、C、D表示);
(2)求摸出两张纸牌牌面上所画几何图形,既是轴对称图形又是中心对称图形的概率.

今年元月,国内一家网络诈骗举报平台发布了《2015年网络诈骗趋势研究报告》,根据报告提供的数据绘制了如下的两幅统计图:
(1)该平台2015年共收到网络诈骗举报多少例?
(2)2015年通过该平台举报的诈骗总金额大约是多少亿元?(保留三个有效数字)
(3)2015年每例诈骗的损失年增长率是多少?
(4)为提高学生的防患意识,现准备从甲、乙、丙、丁四人中随机抽取两人作为受骗演练对象,请用树状图或列表法求恰好选中甲、乙两人的概率是多少?

某小学学生较多,为了便于学生尽快就餐,师生约定:早餐一人一份,一份两样,一样一个,食堂师傅在窗口随机发放(发放的食品价格一样),食堂在某天早餐提供了猪肉包、面包、鸡蛋、油饼四样食品.
(1)按约定,“小李同学在该天早餐得到两个油饼”是 事件;(可能,必然,不可能)
(2)请用列表或树状图的方法,求出小张同学该天早餐刚好得到猪肉包和油饼的概率.
为弘扬中华优秀传统文化,我市教育局在全市中小学积极推广“太极拳”运动.弘孝中学为争创“太极拳”示范学校,今年3月份举行了“太极拳”比赛,比赛成绩评定为A,B,C,D,E五个等级,该校七(1)班全体学生参加了学校的比赛,并将比赛结果绘制成如下两幅不完整的统计图.请根据图中信息,解答下列问题:

(1)该校七(1)班共有 名学生;扇形统计图中C等级所对应扇形的圆心角等于 度;并补全条形统计图;
(2)A等级的4名学生中有2名男生,2名女生,现从中任意选取2名学生作为全班训练的示范者,请你用列表法或画树状图的方法,求出恰好选到1名男生和1名女生的概率.
襄阳市文化底蕴深厚,旅游资源丰富,古隆中、习家池、鹿门寺三个景区是人们节假日玩的热点景区,张老师对八(1)班学生“五•一”小长假随父母到这三个景区游玩的计划做了全面调查,调查分四个类别:A、游三个景区;B、游两个景区;C、游一个景区;D、不到这三个景区游玩.现根据调查结果绘制了不完整的条形统计图和扇形统计图,请结合图中信息解答下列问题:
(1)八(1)班共有学生 人,在扇形统计图中,表示“B类别”的扇形的圆心角的度数为 ;
(2)请将条形统计图补充完整;
(3)若张华、李刚两名同学,各自从三个景区中随机选一个作为5月1日游玩的景区,则他们同时选中古隆中的概率为 .
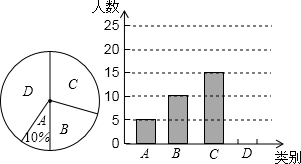
八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类型,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.
类别 |
频数(人数) |
频率 |
小说 |
|
0.5 |
戏剧 |
4 |
|
散文 |
10 |
0.25 |
其他 |
6 |
|
合计 |
|
1 |
根据图表提供的信息,解答下列问题:
(1)八年级一班有多少名学生?
(2)请补全频数分布表,并求出扇形统计图中“其他”类所占的百分比;
(3)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从以上四位同学中任意选出2名同学参加学校的戏剧兴趣小组,请用画树状图或列表法的方法,求选取的2人恰好是乙和丙的概率.

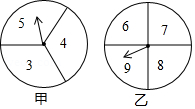
在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
(1)请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;
(2)分别求出李燕和刘凯获胜的概率.
甘肃省省府兰州,又名金城,在金城,黄河母亲河通过自身文化的演绎,衍生和流传了独特的“金城八宝”美食,“金城八宝”美食中甜品类有:味甜汤糊“灰豆子”、醇香软糯“甜胚子”、生津润肺“热冬果”、香甜什锦“八宝百合”;其他类有:青白红绿“牛肉面”、酸辣清凉“酿皮子”、清爽溜滑“浆水面”、香醇肥美“手抓羊肉”,李华和王涛同时去品尝美食,李华准备在“甜胚子、牛肉面、酿皮子、手抓羊肉”这四种美食中选择一种,王涛准备在“八宝百合、灰豆子、热冬果、浆水面”这四种美食中选择一种.(甜胚子、牛肉面、酿皮子、手抓羊肉分别记为A,B,C,D,八宝百合、灰豆子、热冬果、浆水面分别记为E,F,G,H)
(1)用树状图或表格的方法表示李华和王涛同学选择美食的所有可能结果;
(2)求李华和王涛同时选择的美食都是甜品类的概率.
为了解某校九年级全体男生1000米跑步的成绩,随机抽取了部分男生进行测试,并将测试成绩分为 A、 B、 C、 D四个等级,绘制如下不完整的统计图表,如图表所示,根据图表信息解答下列问题:
成绩等级频数分布表
| 成绩等级 |
频数 |
| A |
24 |
| B |
10 |
| C |
x |
| D |
2 |
| 合计 |
y |
(1) x= , y= ,扇形图中表示 C的圆心角的度数为 度;
(2)甲、乙、丙是 A等级中的三名学生,学校决定从这三名学生中随机抽取两名介绍体育锻炼经验,用列表法或画树状图法,求同时抽到甲,乙两名学生的概率.

某中学抽取了40名学生参加"平均每周课外阅读时间"的调查,由调查结果绘制了如下不完整的频数分布表和扇形统计图.
频数分布表
| 组别 |
时间/小时 |
频数/人数 |
| A组 |
0≤ t<1 |
2 |
| B组 |
1≤ t<2 |
m |
| C组 |
2≤ t<3 |
10 |
| D组 |
3≤ t<4 |
12 |
| E组 |
4≤ t<5 |
7 |
| F组 |
t≥5 |
4 |
请根据图表中的信息解答下列问题:
(1)求频数分布表中 m的值;
(2)求 B组, C组在扇形统计图中分别对应扇形的圆心角度数,并补全扇形统计图;
(3)已知 F组的学生中,只有1名男生,其余都是女生,用列举法求以下事件的概率:从 F组中随机选取2名学生,恰好都是女生.

如图,有四张背面完全相同的纸牌 A、 B、 C、 D,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.

(1)从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或树状图)说明理由(纸牌用 A、 B、 C、 D表示).
有四张反面完全相同的纸牌 A、 B、 C、 D,其正面分别画有四个不同的几何图形,将四张纸牌洗匀正面朝下随机放在桌面上.
(1)从四张纸牌中随机摸出一张,摸出的牌面图形是中心对称图形的概率是 .
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张,不放回.再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形既是轴对称图形又是中心对称图形,则小亮获胜,否则小明获胜.这个游戏公平吗?请用列表法(或画树状图)说明理由.(纸牌用 A、 B、 C、 D表示)若不公平,请你帮忙修改一下游戏规则,使游戏公平.

某校调查了若干名家长对"初中生带手机上学"现象的看法,统计整理并制作了如下的条形与扇形统计图,根据图中提供的信息,完成以下问题:
(1)本次共调查了 名家长,扇形统计图中"很赞同"所对应的圆心角度数是 度,并补全条形统计图.
(2)该校共有3600名家长,通过计算估计其中"不赞同"的家长有多少名?
(3)从"不赞同"的五位家长中(两女三男),随机选取两位家长对全校家长进行"学生使用手机危害性"的专题讲座,请用树状图或列表法求出选中"1男1女"的概率.

赤峰市某中学为庆祝"世界读书日",响应"书香校园"的号召,开展了"阅读伴我成长"的读书活动.为了解学生在此次活动中的读书情况,从全校学生中随机抽取一部分学生进行调查,将收集到的数据整理并绘制成如图所示不完整的折线统计图和扇形统计图.

(1)随机抽取学生共 名,2本所在扇形的圆心角度数是 度,并补全折线统计图;
(2)根据调查情况,学校决定在读书数量为1本和4本的学生中任选两名学生进行交流,请用树状图或列表法求这两名学生读书数量均为4本的概率.