初中数学概率公式试题

在一个不透明的袋子中装有除颜色外完全相同的5个红球、3个白球、2个绿球，任意摸出一球，摸到白球的概率是　　．

汤姆斯杯世界男子羽毛球团体赛小组赛比赛规则：两队之间进行五局比赛，其中三局单打，两局双打，五局比赛必须全部打完，赢得三局及以上的队获胜．假如甲，乙两队每局获胜的机会相同．

（1）若前四局双方战成 $2:2$，那么甲队最终获胜的概率是　　；

（2）现甲队在前两局比赛中已取得 $2:0$的领先，那么甲队最终获胜的概率是多少？

小明用 $0-9$中的数字给手机设置了六位开机密码，但他把最后一位数字忘记了，小明只输入一次密码就能打开手机的概率是　　．

（1）某校招聘教师一名，现有甲、乙、丙三人通过专业知识、讲课、答辩三项测试，他们各自的成绩如下表所示：

应聘者	专业知识	讲课	答辩
甲	70	85	80
乙	90	85	75
丙	80	90	85

按照招聘简章要求，对专业知识、讲课、答辩三项赋权 $5:4:1$．请计算三名应聘者的平均成绩，从成绩看，应该录取谁？

（2）我市举行了某学科实验操作考试，有 $A$、 $B$、 $C$、 $D$四个实验，规定每位学生只参加其中一个实验的考试，并由学生自己抽签决定具体的考试实验．小王，小张，小厉都参加了本次考试．

①小厉参加实验 $D$考试的概率是　　；

②用列表或画树状图的方法求小王、小张抽到同一个实验的概率．

为落实立德树人的根本任务，加强思改、历史学科教师的专业化队伍建设．某校计划从前来应聘的思政专业（一名研究生，一名本科生）、历史专业（一名研究生、一名本科生）的高校毕业生中选聘教师，在政治思想审核合格的条件下，假设每位毕业生被录用的机会相等

（1）若从中只录用一人，恰好选到思政专业毕业生的概率是　　 $:$

（2）若从中录用两人，请用列表或画树状图的方法，求恰好选到的是一名思政研究生和一名历史本科生的概率．

将图中的 $A$型、 $B$型、 $C$型矩形纸片分别放在3个盒子中，盒子的形状、大小、质地都相同，再将这3个盒子装入一只不透明的袋子中．

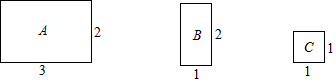
（1）搅匀后从中摸出1个盒子，求摸出的盒子中是 $A$型矩形纸片的概率；

（2）搅匀后先从中摸出1个盒子（不放回），再从余下的两个盒子中摸出一个盒子，求2次摸出的盒子的纸片能拼成一个新矩形的概率（不重叠无缝隙拼接）．

如图，在 $3\times 3$的正方形网格中，有三个小正方形已经涂成灰色，若再任意涂灰1个白色的小正方形（每个白色的小正方形被涂成灰色的可能性相同），使新构成灰色部分的图形是轴对称图形的概率是 $($　　 $)$

A． $\frac{1}{9}$B． $\frac{1}{6}$C． $\frac{2}{9}$D． $\frac{1}{3}$

某十字路口设有交通信号灯，东西向信号灯的开启规律如下：红灯开启30秒后关闭，紧接着黄灯开启3秒后关闭，再紧接着绿灯开启42秒，按此规律循环下去．如果不考虑其他因素，当一辆汽车沿东西方向随机地行驶到该路口时，遇到红灯的概率是　　．

现有五张正面图形分别是平行四边形、圆、等边三角形、正五边形、菱形的卡片，它们除正面图形不同，其它完全相同．将它们背面朝上洗匀后，从中随机抽取一张卡片，卡片的正面图形既是中心对称图形又是轴对称图形的概率是　　．

对于 $▱\mathit{ABCD}$，从以下五个关系式中任取一个作为条件：① $\mathit{AB}=\mathit{BC}$；② $\angle \mathit{BAD}=90°$；③ $\mathit{AC}=\mathit{BD}$；④ $\mathit{AC}\perp \mathit{BD}$；⑤ $\angle \mathit{DAB}=\angle \mathit{ABC}$，能判定 $▱\mathit{ABCD}$是矩形的概率是　　．

为了传承优秀传统文化，某校开展“经典诵读”比赛活动，诵读材料有《论语》，《三字经》，《弟子规》（分别用字母 $A$， $B$， $C$依次表示这三个诵读材料），将 $A$， $B$， $C$这三个字母分别写在3张完全相同的不透明卡片的正面上，把这3张卡片背面朝上洗匀后放在桌面上．小明和小亮参加诵读比赛，比赛时小明先从中随机抽取一张卡片，记录下卡片上的内容，放回后洗匀，再由小亮从中随机抽取一张卡片，选手按各自抽取的卡片上的内容进行诵读比赛．

（1）小明诵读《论语》的概率是　　；

（2）请用列表法或画树状图（树形图）法求小明和小亮诵读两个不同材料的概率．

在不透明的盒子中装有5个黑色棋子和若干个白色棋子，每个棋子除颜色外都相同，任意摸出一个棋子，摸到黑色棋子的概率是 $\frac{1}{4}$，则白色棋子的个数是　　．

在一个不透明的袋子中装有 $n$ 个小球，这些球除颜色外均相同，其中红球有2个，如果从袋子中随机摸出一个球，这个球是红球的概率为 $\frac{1}{3}$ ，那么 $n$ 的值是 $($ 　　 $)$

A．

6

B．

7

C．

8

D．

9

已知一个围棋盒子中装有7颗围棋子，其中3颗白棋子，4颗黑棋子，若往盒子中再放入 $x$颗白棋子和 $y$颗黑棋子，从盒子中随机取出一颗白棋子的概率为 $\frac{1}{4}$，则 $y$与 $x$之间的关系式是　           　．

如图，一个游戏转盘中，红、黄、蓝三个扇形的圆心角度数分别为 $60°$， $90°$， $210°$．让转盘自由转动，指针停止后落在黄色区域的概率是 $($　　 $)$

A． $\frac{1}{6}$B． $\frac{1}{4}$C． $\frac{1}{3}$D． $\frac{7}{12}$