某校为了开阔学生的视野,积极组织学生参加课外读书活动.“放飞梦想”读书小组协助老师随机抽取本校的部分学生,调查他们最喜爱的图书类别(图书分为文学类、艺体类、科普类、其他等四类),并将调查结果绘制成如下两幅不完整的统计图,请你结合图中的信息解答下列问题: 
(1)求被调查的学生人数;
(2)补全条形统计图;
(3)已知该校有1200名学生,估计全校最喜爱文学类图书的学生有多少人?
自从北京举办2008年夏季奥运会以来,奥运知识在我国不断传播,小刚就本班学生的对奥运知识的了解程度进行了一次调查统计.A:熟悉,B:了解较多,C:一般了解.图1和图2是他采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息解答以下问题:
(1)求该班共有多少名学生;(2分)
(2)在条形图中,将表示“一般了解”的部分补充完整.(2’)
(3)在扇形统计图中,计算出“了解较多”部分所对应的圆心角的度数;(2’)
(4)如果全年级共1000名同学,请你估算全年级对奥运知识 “了解较多”的学生人数.(2’)
为宣传节约用水,小明随机调查了某小区部分家庭5月份的用水情况,并将收集的数据整理成如下统计图.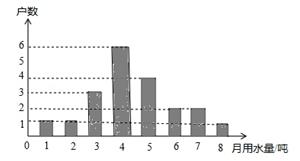
(1)小明一共调查了多少户家庭?
(2)求所调查家庭5月份用水量的众数、平均数;
(3)若该小区有400户居民,请你估计这个小区5月份的用水量.
某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩的原始分均为100分.前6名选手的得分如下:
根据规定,笔试成绩和面试成绩分别按一定的百分比折算成综合成绩(综合成绩的满分仍为100分).
(1)求出这6名选手笔试成绩的中位数、众数;
(2)现得知1号选手的综合成绩为88分,求笔试成绩和面试成绩各占的百分比;
(3)求出其余五名选手的综合成绩,并以综合成绩排序确定前两名人选.
市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
| |
第一次 |
第二次 |
第三次 |
第四次 |
第五次 |
第六次 |
| 甲 |
10 |
8 |
9 |
8 |
10 |
9 |
| 乙 |
10 |
7 |
10 |
10 |
9 |
8 |
(1)根据表格中的数据,分别计算甲、乙的平均成绩;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加省比赛更合适,请说明理由.
(本题8分)某校初三(1)班进行立定跳远训练,以下是李超和陈辉同学六次的训练成绩(单位:m)
| |
1 |
2 |
3 |
4 |
5 |
6 |
| 李超 |
2.50 |
2.42 |
2.52 |
2.56 |
2.48 |
2.58 |
| 陈辉 |
2.54 |
2.48 |
2.50 |
2.48 |
2.54 |
2.52 |
(1)李超和陈辉的平均成绩分别是多少?
(2)分别计算两人的六次成绩的方差,哪个人的成绩更稳定?为什么?
(3)若预知参加级的比赛能跳过2.55米就可能得冠军,应选哪个同学参加?为什么?
某公司为了了解员工每人所创年利润情况,公司从各部抽取部分员工对每年所创年利润情况进行统计,并绘制如图1,图2统计图.
(1)将图补充完整;
(2)本次共抽取员工50 人,每人所创年利润的众数是8万元 ,平均数是 8.12万元;
(3)若每人创造年利润10万元及(含10万元)以上位优秀员工,在公司1200员工中有多少可以评为优秀员工?
某生态示范园要对1号、2号、3号、4号四个品种共500株果树幼苗进行成活实验,从中选出成活率高的品种进行推广,通过实验得知,3号果树幼苗成活率为89.6%,把实验数据绘制成下列两幅统计图(部分信息未给出).

(1)实验所用的2号果树幼苗的数量是 株;
(2)请求出3号果树幼苗的成活数,并把图2的统计图补充完整;
(3)你认为应选哪一种品种进行推广?请通过计算说明理由.
射击集训队在一个月的集训中,对甲、乙两名运动员进行了10次测试,成绩如图(折线图中,粗线表示甲,细线表示乙):

(1)根据图中所提供的信息填写下表:
| |
平均数 |
众数 |
方差 |
| 甲 |
7 |
|
|
| 乙 |
|
|
2.2 |
(2)请从下列四个不同的角度对测试结果进行分析:
①从平均数和方差结合看_______的成绩好;
②从平均数和众数结合看_______的成绩好;
③从折线图上两人射击环数的走势看_____更有潜力.
④如果你是教练,会选择哪位运动员参加比赛?说明理由.
在学统计知识时,老师留的作业是:“请联系自己身边的事物,用所学的统计知识编制一道统计题.”小明就以他们小区的超市每天卖面包的情景编制了如下题目:
某小区超市一段时间每天订购80个面包进行销售,每售出1个面包获利润0.5元,未售出的每个专损0.3元.
(1)若今后每天售出的面包个数用x(0<x≤80)表示,每天销售面包的利润用y(元)表示,写出y与x的函数关系式;
(2)小明连续m天对该超市的面包销量进行统计,并制成了频数分别直方图(每个组距包含左边的数,但不包含右边的数)和扇形统计图,如图1、图2所示,请根据两图提供的信息计算在m天内日销售利润少于32元的天数;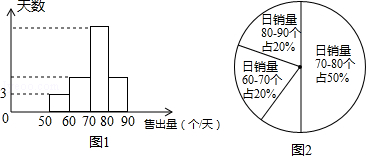
(3)如图(2)中m天内日销售面包个数在70≤x<80这个组内的销售情况如下表:
| 销售量/个 |
70 |
72 |
73 |
75 |
78 |
79 |
| 天数 |
1 |
2 |
3 |
4 |
3 |
2 |
请计算该组内平均每天销售面包的个数.
(本题6分)某校从甲乙两名优秀选手中选一名选手参加全市中学生田径百米比赛(100米记录为12.2秒,通常情况下成绩为12.5秒可获冠军)。该校预先对这两名选手测试了8次,测试成绩如下表:
| |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 选手甲成绩(秒) |
12.1 |
12.4 |
12.8 |
12.5 |
13 |
12.6 |
12.4 |
12.2 |
| 选手乙成绩(秒) |
12 |
11.9 |
12.8 |
13 |
13.2 |
12.8 |
11.8 |
12.5 |
根据测试成绩,请你运用所学过的统计知识做出合理的判断,派哪一位选手参加比赛更好?为什么?
某篮球队在一次联赛中共进行了10场比赛,已知10场比赛的平均得分为88分,且前9场比赛的得分依次为:97、91、85、91、84、86、85、82、88.
(1)求第10场比赛的得分;
(2)求这10场比赛得分的中位数,众数和方差.
某校学生会向全校1900名学生发起了爱心捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为________,图①中m的值是________;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
甲、乙两个小组各10名同学进行英语口语会话练习,各练习5次,他们每个同学合格的次数分别如下:
甲组:4,1,2,2,1,3,3,1,2,1。
乙组:4,3,0,2,1,3,3,0,1,3。
(1).如果合格3次以上(含3次)作为及格标准,请你说明哪个小组的及格率高?
(2).试计算两个小组的方差,请你比较哪个小组的口语会话的合格次数比较稳定?
某校对新入学的七年级部分学生进行了一次视力抽样调查,根据调查的结果,绘制了不完整的频数分布表和频数分布直方图.请根据图表统计信息,解答下列问题:
(1)在频数分布表中,a的值是 ,b的值是 ;并将频数分布直方图补充完整;
(2)这些学生视力的中位数落在频数分布表中的哪个范围内;
(3)若该校七年级共有800名学生,估计该校七年级学生中视力在4.9以上(包括4.9)的学生有多少名?
七年级部分学生视力的频数分布表
视力 频数(人) 频率
4.0≤x<4.3 10 0.1
4.3≤x<4.6 20 0.2
4.6≤x<4.9 35 0.35
4.9≤x<5.2 a 0.3
5.2≤x<5.5 5 b