江苏省泰州市姜堰区九年级上学期期中考试数学试卷
在1:5000的地图上,A、B两地的图上距离为3cm,则A、B两地间实际距离为( )
A.15m B.150m C.1500m D.15000m
两个相似三角形的周长比为1∶4,则它们的对应边上的高比为( )
| A.1∶2 | B.1∶4 | C.1∶8 | D.1∶16 |
已知点C是线段AB的黄金分割点,且AC>BC,则下列等式成立的是( )
| A.AC2=BC·AB | B.AC2=2BC·AB |
| C.AB2=AC·BC | D.BC2=AB·AC |
如图,在□ABCD中,点E为AD的中点,连接BE交AC于点F,则AF∶CF= ( )
| A.1∶2 | B.1∶3 | C.2∶3 | D.2∶5 |
有一人患流感,经过两轮传染后,共有121人患上了流感,那么每轮传染中,平均一个人传染的人数为( )
| A.8人 | B.9人 | C.10人 | D.11人 |
如图,扇形OAB的半径为6cm,AC切弧AB于点A,交OB的延长线点C,若AC=4cm,弧AB的长为3cm,则图中阴影部分面积为 cm2.
已知,方程 .
.
(1)求证:不论 取何值时,方程总有两个不相等实数根;
取何值时,方程总有两个不相等实数根;
(2)若方程有一根为 1,求方程的另一根及
1,求方程的另一根及 的值.
的值.
如图△ABC中,DE∥BC, ,M为BC上一点,AM交DE于N.
,M为BC上一点,AM交DE于N. 
(1)若AE=4,求EC的长;
(2)若M为BC的中点, ,求.
,求. .
.
某篮球队在一次联赛中共进行了10场比赛,已知10场比赛的平均得分为88分,且前9场比赛的得分依次为:97、91、85、91、84、86、85、82、88.
(1)求第10场比赛的得分;
(2)求这10场比赛得分的中位数,众数和方差.
如图,AB是⊙O的切线,切点为B,直线AO交⊙O于点C、D,若∠A=30°.
(1)求∠D的度数;
(2)过C点作⊙O的切线交AB于E,若CE=2,求⊙O的半径.
如图,Rt△ABC中,∠ACB=90°,D是BC的中点,CE⊥AD,垂足为E.
(1)求证:CD2=DE·AD;
(2)求证:∠BED=∠ABC.
矩形ABCD中,AB="6" cm,BC="12" cm ,点P从A出发,沿AB边以1cm/s的速度向点B匀速移动,同时点Q从点B出发,沿BC边以2cm/s的速度向点C匀速移动,设运动时间为t s.
(1)t为何值时,△DPQ的面积等于28cm2;
(2)若DQ⊥PQ时,求t的值;
泰州凤凰城二日游,旅游信息:
根据此旅游信息:某公司组织一批员工到该风景区旅游,支付给旅行社28000元.
(1)你能确定参加这次旅游的人数吗?
(2)若该公司又组织第二批员工到凤凰城旅游并支付给旅行社29250元.如果这两批员工一次性去旅游,则该公司可节约旅游费用多少元?
如图,在⊙O中,AD∥BC,AC⊥BD垂足为E.
(1)求证:BE=CE;
(2)若AD=4,M为AD的中点,延长ME交BC于F,
①判断EF与BC的位置关系;
②求OF的长度.
 ,则
,则 = .
= .
 的值为0,则x= .
的值为0,则x= .
 ,则
,则 = .
= .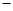 2、2的平均数为 .
2、2的平均数为 .
 (
( )和
)和 (
( )的图象上,OA⊥OB,则
)的图象上,OA⊥OB,则 = .
= .




 粤公网安备 44130202000953号
粤公网安备 44130202000953号