初中数学频数（率）分布直方图试题

为积极响应教育部“停课不停学”的号召，某中学组织本校优秀教师开展线上教学，经过近三个月的线上授课后，在五月初复学．该校为了解学生不同阶段学习效果，决定随机抽取八年级部分学生进行两次跟踪测评，第一次是复学初对线上教学质量测评，第二次是复学一个月后教学质量测评．根据第一次测试的数学成绩制成频数分布直方图（图 $1)$．

复学一个月后，根据第二次测试的数学成绩得到如下统计表：

成绩	$30⩽x<40$	$40⩽x<50$	$50⩽x<60$	$60⩽x<70$	$70⩽x<80$	$80⩽x<90$	$90⩽x⩽100$
人数	1	3	3	8	15	$m$	6

根据以上图表信息，完成下列问题：

（1） $m=$　　；

（2）请在图2中作出两次测试的数学成绩折线图，并对两次成绩作出对比分析（用一句话概述）；

（3）某同学第二次测试数学成绩为78分．这次测试中，分数高于78分的至少有　　人，至多有　　人；

（4）请估计复学一个月后该校800名八年级学生数学成绩优秀 $(80$分及以上）的人数．

为庆祝中国共产党建党100周年，某校开展了以"学习百年党史，汇聚团结伟力"为主题的知识竞赛，竞赛结束后随机抽取了部分学生成绩进行统计，按成绩分成 $A$ ， $B$ ， $C$ ， $D$ ， $E$ 五个等级，并绘制了如下不完整的统计图．请结合统计图，解答下列问题：

等级	成绩     $x$
$A$	$50⩽x<60$
$B$	$60⩽x<70$
$C$	$70⩽x<80$
$D$	$80⩽x<90$
$E$	$90⩽x⩽100$

（1）本次调查一共随机抽取了 　　名学生的成绩，频数分布直方图中 $m=$ 　　；

（2）补全学生成绩频数分布直方图；

（3）所抽取学生成绩的中位数落在 　　等级；

（4）若成绩在80分及以上为优秀，全校共有2000名学生，估计成绩优秀的学生有多少人？

某校积极参与垃圾分类活动，以班级为单位收集可回收垃圾，下面是七年级各班一周收集的可回收垃圾的质量的频数表和频数直方图（每组含前一个边界值，不含后一个边界值）．

某校七年级各班一周收集的可回收垃圾的质量的频数表

组别 $\left(\mathit{kg}\right)$	频数
$4.0~4.5$	2
$4.5~5.0$	$a$
$5.0~5.5$	3
$5.5~6.0$	1

（1）求 $a$的值；

（2）已知收集的可回收垃圾以0.8元 $/\mathit{kg}$被回收，该年级这周收集的可回收垃圾被回收后所得金额能否达到50元？

为了解某校某年级学生一分钟跳绳情况，对该年级全部360名学生进行一分钟跳绳次数的测试，并把测得数据分成四组，绘制成如图所示的频数表和未完成的频数分布直方图（每一组不含前一个边界值，含后一个边界值）．

某校某年级360名学生一分钟跳绳次数的频数表

组别（次     $)$	频数
$100~130$	48
$130~160$	96
$160~190$	$a$
$190~220$	72

（1）求 $a$ 的值；

（2）把频数分布直方图补充完整；

（3）求该年级一分钟跳绳次数在190次以上的学生数占该年级全部学生数的百分比．

为了了解某校九年级学生的跳高水平，随机抽取该年级50名学生进行跳高测试，并把测试成绩绘制成如图所示的频数表和未完成的频数直方图（每组含前一个边界值，不含后一个边界值）．

                    某校九年级50名学生跳高测试成绩的频数表

组别 $\left(m\right)$	频数
$1.09~1.19$	8
$1.19~1.29$	12
$1.29~1.39$	$a$
$1.39~1.49$	10

（1）求 $a$的值，并把频数直方图补充完整；

（2）该年级共有500名学生，估计该年级学生跳高成绩在 $1.29m$（含 $1.29m)$以上的人数．

在4月23日“世界读书日”来临之际，某校为了了解学生的课外阅读情况，从全校随机抽取了部分学生，调查了他们平均每周的课外阅读时间 $t$（单位：小时）．把调查结果分为四档， $A$档： $t<8$； $B$档： $8⩽t<9$； $C$档： $9⩽t<10$； $D$档： $t⩾10$．根据调查情况，给出了部分数据信息：

① $A$档和 $D$档的所有数据是：7，7，7.5，10，7，10，7，7.5，7，7，10.5，10.5；

②图1和图2是两幅不完整的统计图．

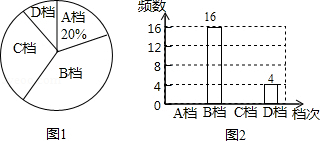
根据以上信息解答问题：

（1）求本次调查的学生人数，并将图2补充完整；

（2）已知全校共1200名学生，请你估计全校 $B$档的人数；

（3）学校要从 $D$档的4名学生中随机抽取2名作读书经验分享，已知这4名学生1名来自七年级，1名来自八年级，2名来自九年级，请用列表或画树状图的方法，求抽到的2名学生来自不同年级的概率．

为了保护视力，学校开展了全校性的视力保健活动，活动前，随机抽取部分学生，检查他们的视力，结果如图所示（数据包括左端点不包括右端点，精确到 $0.1)$；活动后，再次检查这部分学生的视力，结果如表所示．

分组	频数
$4.0⩽x<4.2$	2
$4.2⩽x<4.4$	3
$4.4⩽x<4.6$	5
$4.6⩽x<4.8$	8
$4.8⩽x<5.0$	17
$5.0⩽x<5.2$	5

（1）求所抽取的学生人数；

（2）若视力达到4.8及以上为达标，估计活动前该校学生的视力达标率；

（3）请选择适当的统计量，从两个不同的角度分析活动前后相关数据，并评价视力保健活动的效果．

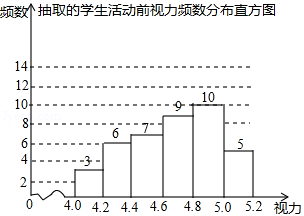
暑期将至，某校组织学生进行"防溺水"安全知识竞赛，老师从中随机抽取了部分学生的成绩（得分取整数，满分为100分），整理后绘制成如图所示的不完整的扇形统计图和频数分布直方图．

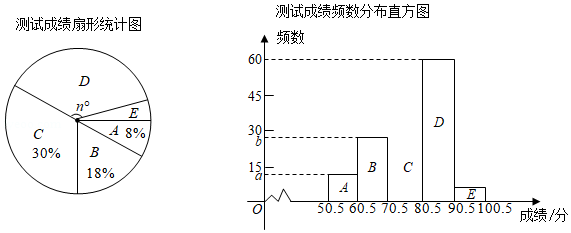
其中 $A$ 组的频数 $a$ 比 $B$ 组的频数 $b$ 小15．请根据以上信息，解答下列问题：

（1）本次共抽取 　　名学生， $a$ 的值为 　　；

（2）在扇形统计图中， $n=$ 　　， $E$ 组所占比例为 　　 $\%$ ；

（3）补全频数分布直方图；

（4）若全校共有1500名学生，请根据抽样调查的结果，估计成绩在80分以上的学生人数．

某网络约车公司近期推出了”520专享”服务计划，即要求公司员工做到“5星级服务、2分钟响应、0客户投诉”，为进一步提升服务品质，公司监管部门决定了解“单次营运里程”的分布情况．老王收集了本公司的5000个“单次营运里程”数据，这些里程数据均不超过25（公里），他从中随机抽取了200个数据作为一个样本，整理、统计结果如下表，并绘制了不完整的频数分布直方图（如图）．

组别	单次营运里程“ $x$”（公里）	频数
第一组	$0<x⩽5$	72
第二组	$5<x⩽10$	$a$
第三组	$10<x⩽15$	26
第四组	$15<x⩽20$	24
第五组	$20<x⩽25$	30

根据统计表、图提供的信息，解答下面的问题：

（1）①表中 $a=$　　；②样本中“单次营运里程”不超过15公里的频率为　　；③请把频数分布直方图补充完整；

（2）请估计该公司这5000个“单次营运里程”超过20公里的次数；

（3）为缓解城市交通压力，维护交通秩序，来自某市区的4名网约车司机 $(3$男1女）成立了“交通秩序维护”志愿小分队，若从该小分队中任意抽取两名司机在某一路口维护交通秩序，请用列举法（画树状图或列表）求出恰好抽到“一男一女”的概率．

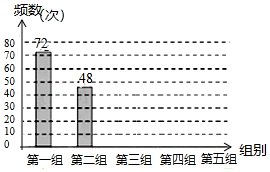
某校"校园主持人大赛"结束后，将所有参赛选手的比赛成绩（得分均为整数）进行整理，并分别绘制成扇形统计图和频数直方图．部分信息如下：

（1）本次比赛参赛选手共有 　 　人，扇形统计图中" $79.5~89.5$ "这一范围的人数占总参赛人数的百分比为 　　；

（2）补全图2频数直方图；

（3）赛前规定，成绩由高到低前 $40\%$ 的参赛选手获奖．某参赛选手的比赛成绩为88分，试判断他能否获奖，并说明理由；

（4）成绩前四名是2名男生和2名女生，若从他们中任选2人作为该校文艺晚会的主持人，试求恰好选中1男1女为主持人的概率．

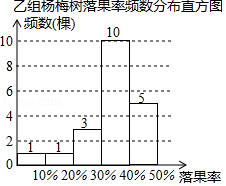
杨梅果实成熟期正值梅雨季节，雨水过量会导致杨梅树大量落果，给果农造成损失．为此，市农科所开展了用防雨布保护杨梅果实的实验研究．在某杨梅果园随机选择40棵杨梅树，其中20棵加装防雨布（甲组），另外20棵不加装防雨布（乙组）．在杨梅成熟期，统计了甲、乙两组中每一棵杨梅树的落果率（落地的杨梅颗数占树上原有杨梅颗数的百分比），绘制成统计图表（数据分组包含左端值不包含右端值）．

甲组杨梅树落果率频数分布表

落果率	组中值	频数（棵     $)$
$0⩽x<10\%$	$5\%$	12
$10\%⩽x<20\%$	$15\%$	4
$20\%⩽x<30\%$	$25\%$	2
$30\%⩽x<40\%$	$35\%$	1
$40\%⩽x<50\%$	$45\%$	1

（1）甲、乙两组分别有几棵杨梅树的落果率低于 $20\%$ ？

（2）请用落果率的中位数或平均数，评价市农科所"用防雨布保护杨梅果实"的实际效果；

（3）若该果园的杨梅树全部加装这种防雨布，落果率可降低多少？说出你的推断依据．

某校为了增强学生的疫情防控意识，组织全校2000名学生进行了疫情防控知识竞赛．从中随机抽取了 $n$ 名学生的竞赛成绩（满分100分），分成四组： $A:60⩽x<70$ ； $B:70⩽x<80$ ； $C:80⩽x<90$ ； $D:90⩽x⩽100$ ，并绘制出不完整的统计图：

（1）填空： $n=$ 　　；

（2）补全频数分布直方图；

（3）抽取的这 $n$ 名学生成绩的中位数落在 　　组；

（4）若规定学生成绩 $x⩾90$ 为优秀，估算全校成绩达到优秀的人数．

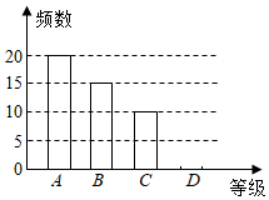
某校开展主题为"防疫常识知多少"的调查活动，抽取了部分学生进行调查，调查问卷设置了 $A$ ：非常了解、 $B$ ：比较了解、 $C$ ：基本了解、 $D$ ：不太了解四个等级，要求每个学生填且只能填其中的一个等级，采取随机抽样的方式，并根据调查结果绘制成如图所示不完整的频数分布表和频数分布直方图，根据以上信息回答下列问题：

等级	频数	频率
$A$	20	0.4
$B$	15	$b$
$C$	10	0.2
$D$	$a$	0.1

（1）频数分布表中 $a=$ 　　， $b=$ 　　，将频数分布直方图补充完整；

（2）若该校有学生1000人，请根据抽样调查结果估算该校"非常了解"和"比较了解"防疫常识的学生共有多少人？

（3）在"非常了解"防疫常识的学生中，某班有5个学生，其中3男2女，计划在这5个学生中随机抽选两个加入防疫志愿者团队，请用列表或画树状图的方法求所选两个学生中至少有一个女生的概率．

某养猪场对200头生猪的质量进行统计，得到频数直方图（每一组含前一个边界值，不含后一个边界值）如图所示，其中质量在 $77.5\mathit{kg}$及以上的生猪有　　头．

红星中学课外兴趣活动小组对某水稻品种的稻穗谷粒数目进行调查，从试验田中随机抽取了30株，得到的数据如下（单位：颗） $:$

182	195	201	179	208	204	186	192	210	204
175	193	200	203	188	197	212	207	185	206
188	186	198	202	221	199	219	208	187	224

（1）对抽取的30株水稻稻穗谷粒数进行统计分析，请补全下表中空格，并完善直方图：

谷粒颗数	$175⩽x<185$	$185⩽x<195$	$195⩽x<205$	$205⩽x<215$	$215⩽x<225$
频数		8	10		3
对应扇形 图中区域		$D$	$E$		$C$

如图所示的扇形统计图中，扇形 $A$对应的圆心角为　　度，扇形 $B$对应的圆心角为　　度；

（2）该试验田中大约有3000株水稻，据此估计，其中稻穗谷粒数大于或等于205颗的水稻有多少株？